El presente texto tiene más de 40 años de haber sido escrito y fue pensado como un curso introductorio a la Topología de Conjuntos. Está dirigido pues a estudiantes de licenciatura y ha sido utilizado en diferentes tiempos y lugares, tanto por profesores y estudiantes en cursos propios de estos temas como por lectores autodidactas y como material de consulta por matemáticos profesionales.

Inicialmente, se presenta a los espacios topológicos en su mayor generalidad y a los productos de tales espacios. Después, a los espacios cocientes, los cuales resultan de partir a los espacios originales mediante relaciones de equivalencia entre sus miembros. La topología cociente es precisamente la más fina que hace continua a la proyección canónica. De manera muy elegante, se expone la teoría de filtros con el propósito de introducir la noción de convergencia dentro de espacios topológicos. Se pasa a revisar la teoría de los espacios que cumplen con la caracterización de separabilidad debida a Hausdorff, a saber: para cualquier pareja de puntos distintos, existen sendas vecindades de ellos que son ajenas; vale decir, espacios del tipo T₂. Después se estudia a los espacios regulares, o sea, aquellos separados en los que cada conjunto cerrado puede ser separado de cualquier punto fuera de él por sendas vecindades del cerrado y del punto; también conocidos como espacios del tipo T₃. Luego se ve la noción de compacidad, tanto desde la caracterización de Borel-Lebesgue, como en los casos particulares de los espacios métricos y de los espacios reales. Se ve aquí la compactificación de Alexándrov, los espacios localmente compactos y entre éstos los numerables en el infinito. Luego se ve la noción de conexidad, los espacios conexos, los localmente conexos y los conexos por arcos, así como las relaciones entre ellos. El penúltimo capítulo está dedicado a los espacios normales, los cuales son separados tales que para cualquier pareja de conjuntos cerrados ajenos existen sendas vecindades ajenas que los contienen también conocidos como espacios del tipo T₄. Aquí se muestra el Lema de Uryson, el Teorema de Tietze-Uryson y la caracterización de los espacios metrizables. Finalmente se presenta a los Teoremas de Stone-Weierstrass. Se estudia a los espacios de funciones reales continuas definidas sobre compactos y su estructura como álgebras de Banach, y a los espacios de funciones reales nulas en el infinito sobre espacios localmente compactos. Se muestra que en estos espacios ciertas familias de funciones que separan puntos son densas, lo que entraña que, en el caso de los espacios de funciones continuas en compactos, los conjuntos de polinomios son densos.

Una componente muy importante del presente curso está constituida por sus ejercicios. El lector encontrará que éstos, con diversos niveles de dificultad, amplían sustancialmente el contenido del curso y presentan enfoques alternativos a los expuestos en el texto. Invitamos a los lectores a que se esfuercen en resolverlos y no los desdeñen.

Agradezco a José María Rocha, de la Escuela Superior de Física y Matemáticas del IPN (ESFM-IPN), y a Miguel A. Xicoténcatl, del Departamento de Matemáticas del Cinvestav-IPN, el que me hayan facilitado material suplementario, manuscritos originales del prof. Biberstein, para la preparación de la presente edición de este curso de Topología de Conjuntos. Igualmente manifiesto mi agradecimiento a Edgar González, del Departamento de Computación del Cinvestav-IPN, por haber trazado la mayoría de los dibujos que aparecen en esta edición. Agradezco a Miguel Tufiño Velázquez, Director de la ESFM-IPN, su apoyo entusiasta para publicar el presente texto, y a Erick Lee Guzmán, Jefe del Departamento de Matemáticas en esa misma escuela, su interés en este libro. Igualmente, agradezco el apoyo del personal de la propia Dirección de Publicaciones del IPN y las cuidadosas observaciones de los revisores anónimos de la presente obra (por supuesto, los errores que hayan persistido son de mi responsabilidad exclusiva).

En septiembre de 2016 tuve oportunidad de visitar las ciudades de Leópolis y Drohobycz, situadas en la región de Galicja, en la actualidad en la parte occidental de Ucrania, pero que en el período de entreguerras fue una parte de la República de Polonia. Leópolis fue un centro muy importante de cultura polaca y ahí floreció el célebre grupo de matemáticos polacos de antes de la Segunda Guerra Mundial, cuyo miembro prominente fue el gran Stefan Banach. El Café Escocés, ubicado en el centro de esa ciudad, es un lugar legendario para la historia de las matemáticas del S. XX. Me permito incluir algunas fotos de ese Café y de la tumba de Banach. En Drohobycz nació el prof. Biberstein y aunque él en alguna ocasión me manifestó que desde temprana edad vivió fuera de la comunidad judía en la que nació, incluyo aquí fotos actuales de esa ciudad mostrando su sinagoga y la casa del poeta y pintor Bruno Schulz, quien fuera profesor de dibujo de Biberstein en la escuela secundaria, y un gran intelectual y artista representativo tanto de la cultura judía como de la cultura polaca.

Agradezco en especial a los señores Zbygniew y Zofia (Sonia) Figas el que me hayan acompañado en ese viaje, junto con mi hija Laura, y que me hayan facilitado que en apenas cuatro días haya podido yo apreciar personalmente los vestigios de la grandeza de la cultura polaca en esas tierras.

Coloco álbumes de fotos de ese viaje por lares de origen del prof. Biberstein, los cuales pueden ser consultados mediante los sitios en Internet indicados:
http://img.gg/YNkFPv8     Ciudad de Leópolis, con el Café Escocés
http://img.gg/x9aw96P     Cementerio Łyczakowski en Leópolis, con el Memorial Orlat de los Defensores de Polonia
http://img.gg/lONKCMI     Ciudad de Drohobycz
http://img.gg/grSw2NB     Antigua iglesia de madera de San Jorge en Drohobycz

Guillermo Morales-Luna
gmorales@cs.cinvestav.mx

Preface

This course has been prepared fourty years ago as a textbook in Set Topology, it has been addressed to undergraduate students in Mathematics, it has been used in several places and times, and it has been also used as a handbook for professionals in other areas.

Initially topological spaces are introduced in a general way, and the notion of product spaces is introduced as well. Then, quotient spaces are defined in terms of the finest topology that makes the canonical projections continuous. In a rather elegant way, filters are exposed with the purpose to analyze the notion of convergence in topological spaces. Then, in an approach related to separability, the T₂ spaces are studied, namely the spaces satisfying Hausdorffs axiom: any two different points may be separated by corresponding disjoint neighborhoods. Thereafter, regular or T₃ spaces are studied, namely those separable spaces in which any closed set can be separated of any outside point by corresponding disjoint open heighborhoods. Then the notion of compactness is introduced, in a general setting according to the Borel-Lebesgue axiom, and in the particular cases of metric spaces and the real line. Alexandrovs compactification is introduced here, as well as the locally compact spaces and the spaces countable at the infinity. The notion of connectedness follows: the connected spaces, the locally connected spaces and the path-connected spaces, as well as the relations among them. The before last chapter is devoted to normal or T₄ spaces, in which any two disjoint closed sets can be separated by corresponding disjoint open neighborhoods. Here Uryshons Lemma and the Tietze-Uryshon Theorem are proved, and the metrizable space are characterized. Finally, the Stone-Weierstrass Theorems are presented. The spaces of continuous real maps over compact sets and the spaces of continuous maps converging to zero at infinity in locally compact spaces are studied as Banach algebras, and it is shown that certain function subsets separating points are dense, which entails that, in the case of continuous maps over compact sets, the sets of polynomials are dense.

An important component of the current text consists of the proposed exercises. The reader is encouraged to solve them entirely, there, the reader will find some extensions of the exposed theory or alternative approaches to the stated results.

Special thanks are due to my colleagues, José María Rocha, from the Physics and Mathematics School (ESFM) of Mexican National Polytechnic Institute (IPN) and Miguel A. Xicoténcatl, from the Mathematics Department of Cinvestav-IPN, since they provided me with original manuscripts of prof. Biberstein of great help in the preparation of the current edition of this course. Also I thank Edgar González, from the Computer Science Department of Cinvestav-IPN, for most of the picture plots appearing in this edition. I am grateful as well to Miguel Tufiño Velázquez, Director of the ESFM-IPN, for his enthusiastic support to publish this book, and to Erick Lee Guzmán, Chairman at the Mathematics Department of ESFM-IPN. I thank also the personal at the Publishing Direction of IPN and the careful remarks of the anonymous referees of this book (evidently the still subsistent mistakes are my sole responsability).

In September, 2016, I visited the cities of Lviv and Drohobycz, in the former Galician Region of the Polish Kingdom, later part of the Austro-Hungarian Empire of the XIX Century, then a part of the Republic of Poland, and at present time in the western part of Ucrania. In the period between de World Wars of the XX Century, Lviv was an imporant center of Polish culture and there fluorished an important group of talented mathematicians, leaded by Stefan Banach. The Scotish Café, in the center of Lviv, was a meeting place of this group, and it is a legendary lieu in the worldwide History of Mathematics. I include a couple of recent pictures of the Scotish Café and the grave of Stefan Banach. In Drohobycz, prof. Biberstein was born and though he told me personally once that he was a youngster when he exited the closed Jewish communities of his childhood, I am including here recent photos of the city sinagogue and the house of Bruno Schulz, who was teacher of Biberstein in Art at the secondary school. Schulz was a reputed poet and artist quite representative of the Polish culture and the Jewish culture developed in Galicia, and he was killed by the Nazis during Lvivs occupation in World War II.

Special thanks as well are due to Mr. Zbygniew and Mrs. Zofia (Sonia) Figas because they accompanied and guided me during that trip, together with my daughter Laura. Without their effort and patience, I could not visit so many places in a short time. They give me the opportunity to appreciate by myself the current vestiges of the greatness of Polish culture heritage on that region.

I share photo albums of the September, 2016, tour through the lands of origin of prof. Biberstein. They can be reached through the following Internet locations:
http://img.gg/YNkFPv8 Lviv and the Scotish Café
http://img.gg/x9aw96P Łyczakowski cementary in Lviv and the Memorial Orlat of the Polish Defenders
http://img.gg/lONKCMI Drohobycz
http://img.gg/grSw2NB Old wooden church of Saint George in Drohobycz

Guillermo Morales-Luna
gmorales@cs.cinvestav.mx

Przedmowa

Tekst ten napisany został przeszło 40 lat temu jako kurs wstȩpny w dziedzinie Topologii Zbiorów. Skierowany jest wiȩc do studentów poziomu licencjackiego. W różnych czasach i miejscach, korzystali z niego jako materiału do konsultacji tak wykładowcy jak studenci na zajȩciach zwi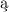zanych z tym tematem, samoucy, czy też matematycy profesjonaliści.

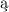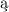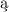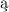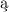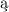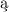Na pocztku przedstawia siȩ przestrzenie topologiczne w sposób bardzo ogólny, jak też produkty tych przestrzeni. Nastȩpnie, przestrzenie ilorazowe, wynikajce z podziału przestrzeni oryginalnych przez relacje równoważności miȩdzy jej elementami. Topologia ilorazowa jest t najbogatsz dziedzin, nadajc ci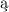głość odwzorowaniu rzutowemu. W bardzo elegancki sposób przedstawia siȩ teoriȩ filtrów w celu wprowadzenia pojȩcia zbieżności w przestrzeniach topologicznych. Nastȩpnie opisuje siȩ teoriȩ przestrzeni spełniaj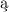cych cechy rozł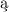czności opracowan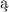 przez Hausdorffa, a mianowicie: dla jakiejkolwiek pary różnych punktów istniej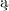 osobne zbiory otwarte tych punktów, które s 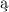oddzielne; to znaczy, przestrzenie typu T₂. Z kolei bada przestrzenie regularne, to znaczy oddzielne, w których każdy domkniȩty zbiór może być oddzielony od jakiegokolwiek punktu poza nim przez oddzielne zbiory otwarte, znane też jako przestrzenie typu T₃. Nastȩpnie analizuje siȩ pojȩcie przestrzeni zwartej, tak z punktu widzenia charakterystyki Borela-Lebesguea, jak w szczególnych przypadkach przestrzeni metrycznych oraz przestrzeni rzeczywistych. Obserwujemy tu uzwarcenie Aleksandrowa, przestrzenie lokalnie zwarte i wśród nich przeliczalne w nieskończoności. Kolejno przedstawia siȩ pojȩcie spójności, przestrzenie spójne, spójności lokalne oraz drogowo spójne, jak też wzajemne ich relacje. 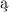Przedostatni rozdział poświȩcony jest przestrzeniom normalnym, które s oddzielne, tak że dla jakiejkolwiek pary zbiorów domkniȩtych oddzielnych istniej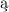 oddzielne zbiory otwarte je zawieraj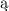ce, znane również jako przestrzenie typu T₄. Przedstawia siȩ tutaj Lemat Urysona, Twierdzenie Tietze-Urysona oraz charakterystykȩ przestrzeni metryzowanych. Na koniec przedstawia siȩ Twierdzenie Stona-Weierstrassa. Analizuje siȩ przestrzenie funkcji rzeczywistych ci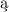głych określonych na przestrzeniach zwartych oraz ich strukturȩ jako algebrȩ Banacha, jak też przestrzenie funkcji rzeczywistych nieważnych w nieskończoności w przestrzeniach lokalnie zwartych. Wykazuje siȩ, że w tych przestrzeniach pewne rodziny funkcji oddzielaj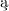cych punkty to zbiory gȩste, co zadziwia, iż w przypadku zespołów funkcji ci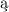głych w przestrzeniach zwartych, zbiory wielomianów s zbiorami gȩstymi.

Na bardzo istotny element tego materiału składaj siȩ ćwiczenia. Lektor przekona siȩ, iż ćwiczenia, o różnym poziomie trudności, rozszerzaj w znaczcej mierze zawartość kursu i oferuj alternatywne punkty widzenia na te, które zostały przedstawione w tekście. Zapraszam czytelników do ich nie lekceważenia, do włożenia wysiłku w celu ich rozwizywania.

Składam podziekowania doktorowi José María Rocha z Wyższej Szkoły Fizyki i Matematyki Narodowego Instytutu Politechnicznego (ESFM-IPN) oraz doktorowi Miguelowi A. Xicoténcatl z Wydziału Matematyki Cinvestav-IPN, za użyczenie mi dodatkowych materiałów w postaci oryginalnych rȩkopisów profesora Bibersteina, wykorzystanych do przygotowania niniejszej edycji kursu Topologii Zbiorów. Równocześnie pragnȩ wyrazić moje podziȩkowania magistrowi Edgarowi Gonzalezowi z Wydziału Informatyki Cinvestav-IPN, za wykonanie wiȩkszości rysunków zamieszczonych w niniejszym wydaniu. Składam wyrazy podziȩkowania panu Miguelowi Tufiño Velázquezowi, Dyrektorowi ESFM-IPN, za jego entuzjastyczne wsparcie przy publikacji niniejszego tekstu, oraz panu Erikowi Lee Guzmanowi, Kierownikowi Wydziału Matematyki wymienionej wyżej Uczelni, za zainteresowanie t ksiżk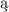. Równocześnie dziȩkujȩ pracownikom Dyrekcji d/s Publikacji meksykańskiej Politechniki, za ich wsparcie oraz za celne uwagi anonimowym recenzentom niniejszej pracy (za błȩdy, kóre mogły pozostać, ponoszȩ oczywiście wył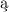czn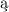 odpowiedzialność).

We wrześniu 2016 roku miałem okazjȩ zwiedzić miasta Lwów i Drohobycz, położone w regionie galicyjskim, obecnie zachodniej czȩści Ukrainy, lecz w okresie miȩdzywojennym należ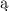cym do Rzeczypospolitej Polskiej. Lwów stanowił bardzo ważny ośrodek polskiej kultury i tam właśnie, przed wybuchem Drugiej Wojny Światowej, powstała słynna grupa polskich matematyków, której wybitnym członkiem był wielki Stefan Banach. Kawiarnia Szkocka, położona w centrum miasta, jest miejscem legendarnym w światowej historii matematyki XX wieku. Pozwoliłem sobie załczyć kilka zdjȩć z tej kawiarni oraz zdjȩcie grobu Banacha. W Drohobyczu urodził siȩ profesor Olgierd Alf Biberstein i choć, przy jakiejś okazji powiedział mi, iż od najmłodszych lat żył poza żydowsk społeczności w której przyszedł na świat, załczam aktualne zdjȩcia tego miasta, z jego synagog oraz domem poety i malarza Bruno Schultza, który był nauczycielem rysunku Bibersteina w szkole średniej, wielkim intelektualist i artyst reprezentatywnym tak dla kultury żydowskiej jak dla polskiej kultury.

Składam specjalne podziekowania państwu Zbigniewowi i Zofii (Sonii) Figas za towarzyszenie mi w tej podróży, wraz z moj córk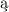 Laur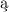; dzieki nim w ci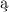gu zaledwie czterech dni miałem możliwość poznać osobiście ślady wielkiej polskiej kultury na tych ziemiach.

Zamieszczam zdjȩcia z mej podróży w miejsca pochodzenia profesora Bibersteina, których wiȩcej można zobaczyć na nastȩpuj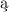cych stronach internetowych:
http://img.gg/YNkFPv8     Miasto Lwów z Kawiarni Szkock
http://img.gg/x9aw96P     Cmentarz Łyczakowski w Lwowie, z memoriałem Orlt Obrońców Polski
http://img.gg/lONKCMI     Miasto Drohobycz
http://img.gg/grSw2NB    Stara drewniana cerkiew Św. Jerzego w Drohobyczu

Guillermo Morales-Luna
gmorales@cs.cinvestav.mx

(Opracowanie tekstu polskiego: Małgorzata Hadryś-Luna.)

TOPOLOGÍA DE CONJUNTOS:

Un enfoque debido a O. A. Biberstein

Contenido

Prefacio

Preface

Przedmowa