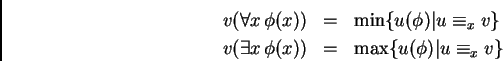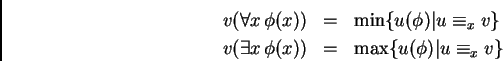Siguiente: Problema fundamental de la Un nivel arriba: Introducción a la lógica Anterior: Cálculo proposicional difuso

Cálculo de predicados difuso

De igual manera a como se procede en el cálculo de predicados clásico, se supone dada una signatura, consistente de una colección de constantes, una colección de relaciones y una colección de funciones. Cada relación $R$ y cada función $F$ tiene asociada una aridad, es decir, un número de argumentos. Los términos se forman considerando a las constantes y a las variables como términos y a la composición de símbolos de funciones con términos, como términos también. Las fórmulas atómicas se obtienen como composición de símbolos de relaciones con términos. Las fórmulas se obtienen considerando como tales a las fórmulas atómicas, a la composición de fórmulas con conectivos lógicos y a las cuantificaciones universales y existenciales de fórmulas (véase los detalles de construcción en el escrito de José Alfredo Amor en este mismo libro). También, al igual que en el caso clásico, una interpretación consiste de un universo $M$, de una correspondencia de cada constante $c$ en la signatura con un elemento $m_c$ en $M$ y de una correspondencia de símbolos de funciones con funciones en $M$: Si $f$ es un símbolo de función de aridad $n$, entonces $m_f$ es una función con dominio $M^n$ y contradominio $M$, es decir, $m_f:M^n\to M$. De esta manera, a cada término $t$ que no involucre variables, le corresponderá un elemento $m_t$ en $M$. Para completar la noción de interpretación, a cada símbolo de relación $R$, digamos que de aridad $n$, se le asocia un conjunto difuso $m_R$ en el universo $M^n$; y a los conectivos lógicos se les asocia funciones específicas de evaluación. Pues bien, una asignación $v$ asocia a cada variable $x$ un elemento en $M$ (escribiremos $v\equiv_x u$ para denotar el hecho de que $v$ y $u$ coinciden en todas las variables, excepto, quizá, en $x$). A una fórmula atómica cerrada, es decir sin variables, $R(t_1,\ldots,t_n)$ la asignación le asocia como valor de verdad el grado de pertenencia de la $n$-ada $(m_{t_1},\ldots,m_{t_n})$ al conjunto difuso $m_R$. En símbolos: $v(R(t_1,\ldots,t_n))=g_{m_R}(m_{t_1},\ldots,m_{t_n}).$ Si $\Box$ es un conectivo lógico, con función de evaluación $f_{\Box}$ entonces para dos fórmulas $\phi$, $\psi$ se define $v(\phi\Box\psi) = f_{\Box}(v(\phi),v(\psi))$. Finalmente, para fórmulas cuantificadas se define:

$$\begin{eqnarray*} v(\forall x \phi(x)) &=& \min\{u(\phi)\vert u\equiv_x v\} \... ...\exists x \phi(x)) &=& \max\{u(\phi)\vert u\equiv_x v\} %%\\ \end{eqnarray*}$$

Así pues, ya sea en un cálculo difuso de proposiciones o en uno de predicados, se puede plantear los siguientes dos problemas:

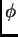
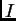
Problema 4.1 (de deducción o de ``pronóstico'')   Para una fórmula $\phi$, si se sabe que las fórmulas atómicas que involucra toman valores de verdad en ciertos intervalos, entonces se ha de estimar en qué intervalo $I$ ha de caer el valor de verdad de $\phi$.

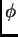
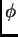
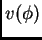
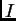
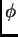
Problema 4.2 (de inferencia o de ``diagnóstico'')   Para una fórmula $\phi$, si se sabe que el valor de verdad $v(\phi)$ cae en un intervalo $I$, y que para algunos átomos involucrados en $\phi$ sus correspondientes valores de verdad caen en ciertos intervalos, entonces se ha de estimar para los átomos restantes en qué intervalos debieron caer sus correspondientes valores de verdad.

Siguiente: Problema fundamental de la Un nivel arriba: Introducción a la lógica Anterior: Cálculo proposicional difuso