



Siguiente: Jerarquía de Chomsky
Un nivel arriba: Introducción a la teoría
Anterior: Algoritmos de Markov
Sea T un conjunto de símbolos terminales y sea V un conjunto de símbolos variables. La unión de ellos,
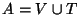 ,
es un alfabeto de gramática. A* es el diccionario sobre A y consta de todas las palabras, de longitud finita, con símbolos en A. A+ coincide con A*, salvo en que no posee a la palabra vacía,
,
es un alfabeto de gramática. A* es el diccionario sobre A y consta de todas las palabras, de longitud finita, con símbolos en A. A+ coincide con A*, salvo en que no posee a la palabra vacía,
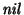 .
Una regla de producción es un elemento del producto cartesiano
.
Una regla de producción es un elemento del producto cartesiano
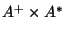 .
Si
.
Si
 escribimos
escribimos
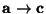 y decimos que
y decimos que
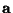 es el antecedente y
es el antecedente y
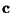 el consecuente de la regla
el consecuente de la regla
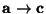 .
Sea
.
Sea
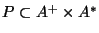 un conjunto de reglas de producción. Sea
un conjunto de reglas de producción. Sea 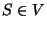 un símbolo variable distinguido, llamado inicial.
El sistema
G = (V, T, P, S) se dice ser una gramática formal.
Las reglas de producción transforman palabras en otras:
un símbolo variable distinguido, llamado inicial.
El sistema
G = (V, T, P, S) se dice ser una gramática formal.
Las reglas de producción transforman palabras en otras:
La cerradura reflexivo-transitiva de la relación ``da'' define la relación de derivación
El lenguaje generado por la gramática consta de todas las palabras que se derivan del símbolo inicial y que sólo contienen símbolos terminales:




Siguiente: Jerarquía de Chomsky
Un nivel arriba: Introducción a la teoría
Anterior: Algoritmos de Markov
Guillermo Morales-Luna
2000-06-27