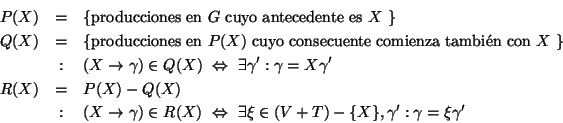Siguiente: Forma normal de Greibach
Un nivel arriba: Formas normales
Anterior: Formas normales
Una gramática libre de contexto
G=(V,T,P,S) se dice estar en forma normal de Chomsky si sus producciones son de cualquiera de las dos formas
Proposición 3.1
Toda gramática libre de contexto
G=(V,T,P,S) que no genere a la palabra vacía se puede transformar en una gramática libre de contexto
G'=(V',T,P',S') en forma normal de Chomsky.
En efecto, dada una gramática G, apliquemos el último procedimiento de la sección anterior para transformar a G en una gramática G'' sin variables inútiles ni producciones vacías ni producciones unitarias equivalente a G.
A las producciones que quedasen de la forma
 con
con 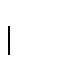 y
y 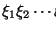 las dejamos sin cambio alguno.
A cada producción de la forma
las dejamos sin cambio alguno.
A cada producción de la forma
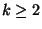 ,
con
,
con
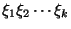 y
y 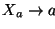 ,
la transformamos en una sucesión de producciones de la forma siguiente:
A cada símbolo terminal
,
la transformamos en una sucesión de producciones de la forma siguiente:
A cada símbolo terminal 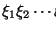 que aparezca en la palabra
que aparezca en la palabra
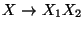 le asociamos una variable nueva Xa e incorporamos la producción
le asociamos una variable nueva Xa e incorporamos la producción
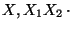 .
Así pues las producciones que no sean de la forma
.
Así pues las producciones que no sean de la forma
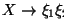 con X variable y a terminal, han de ser de la forma
con X variable y a terminal, han de ser de la forma
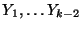 ,
con
,
con
 todos variables. Para cada una de estas últimas producciones introducimos k-2 nuevas variables
todos variables. Para cada una de estas últimas producciones introducimos k-2 nuevas variables
 e incorporamos la sucesión de producciones
e incorporamos la sucesión de producciones
Obtenemos así la forma normal equivalente a la gramática dada.




Siguiente: Forma normal de Greibach
Un nivel arriba: Formas normales
Anterior: Formas normales
Guillermo Morales-Luna
2000-06-27
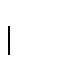 y
y 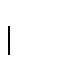 y
y 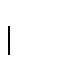 y
y  todos variables. Para cada una de estas últimas producciones introducimos k-2 nuevas variables
todos variables. Para cada una de estas últimas producciones introducimos k-2 nuevas variables
 e incorporamos la sucesión de producciones
e incorporamos la sucesión de producciones