



Siguiente: Monoide de cadenas
Un nivel arriba: Fundamentos matemáticos
Anterior: Fundamentos matemáticos
El producto cartesiano de dos conjuntos A y B consta de las parejas ordenadas cuyo primer elemento está en A y cuyo segundo elemento está en B. Usaremos la notación de yuxtaposición para denotar al producto cartesiano:
Cualquier conjunto finito 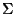 es un alfabeto. Entre los alfabetos más comunes están:
es un alfabeto. Entre los alfabetos más comunes están:
Sea
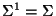 y, para
y, para 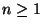 ,
sea
,
sea
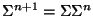 .
Cada elemento
.
Cada elemento
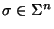 se dice ser una palabra sobre
se dice ser una palabra sobre 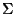 de longitud n. La palabra
de longitud n. La palabra
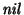 que no tiene símbolo alguno es la palabra vacía. Definimos
que no tiene símbolo alguno es la palabra vacía. Definimos
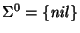 .
El diccionario sobre
.
El diccionario sobre 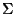 es
es
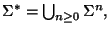 y, por ende, consta de todas las palabras de longitud finita con símbolos en el alfabeto
y, por ende, consta de todas las palabras de longitud finita con símbolos en el alfabeto 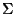 .
El conjunto de palabras no-vacías, se denota como
.
El conjunto de palabras no-vacías, se denota como
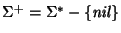 .
Para cada
.
Para cada 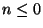 ,
,
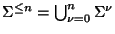 es el conjunto de palabras de longitud a lo sumo n.
es el conjunto de palabras de longitud a lo sumo n.
Ejemplos:
- 1.
-
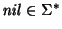 para cualquier alfabeto
para cualquier alfabeto 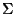 .
.
- 2.
-
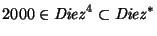 .
.
- 3.
-
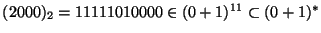 .
.
- 4.
-
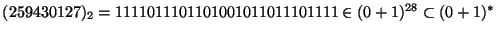 .
.
- 5.
-
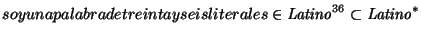 .
.
- 6.
- Cualquier programa en C es una palabra en
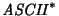 .
.
Un lenguaje es un subconjunto de cualquier diccionario. 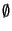 y
y 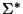 son los lenguajes vacío y total, respectivamente.
son los lenguajes vacío y total, respectivamente.




Siguiente: Monoide de cadenas
Un nivel arriba: Fundamentos matemáticos
Anterior: Fundamentos matemáticos
Guillermo Morales-Luna
2000-06-27
