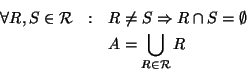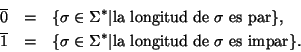


Siguiente: Propiedades de lenguajes
Un nivel arriba: Monoide de cadenas
Anterior: Homomorfismos
En un conjunto A, una relación de equivalencia R es un subconjunto
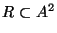 tal que es
tal que es
- reflexiva:
 ,
,
- simétrica:
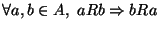 ,
y
,
y
- transitiva:
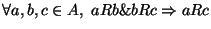 .
.
Una relación de equivalencia induce una partición de manera natural: Para cada elemento 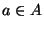 la clase de equivalencia de a bajo la relación R es el conjunto
la clase de equivalencia de a bajo la relación R es el conjunto
![$[a]_R=\{b\in A\vert aRb\}$](img262.gif) que consta de los elementos equivalentes a a. Se tiene
que consta de los elementos equivalentes a a. Se tiene
Así pues, la colección de clases de equivalencia
![$A/R=\{[a]_R\vert a\in A\}$](img264.gif) es una partición de A. A/R se dice ser el cociente de A bajo la relación R. La cardinalidad del cociente A/R es el índice de la relación R. La función
es una partición de A. A/R se dice ser el cociente de A bajo la relación R. La cardinalidad del cociente A/R es el índice de la relación R. La función
![$\pi_R:a\mapsto [a]_R$](img265.gif) ,
que a cada elemento le asocia su clase de equivalencia, es la proyección canónica de A sobre el cociente A/R.
Toda relación de equivalencia induce pues una partición en su conjunto de definición. Recíprocamente, si
,
que a cada elemento le asocia su clase de equivalencia, es la proyección canónica de A sobre el cociente A/R.
Toda relación de equivalencia induce pues una partición en su conjunto de definición. Recíprocamente, si 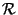 es una partición en A, es decir, si
es una partición en A, es decir, si 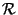 es una colección de subconjuntos de A tal que
es una colección de subconjuntos de A tal que
entonces la relación
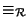 definida como
definida como
es una relación de equivalencia que determina como cociente precisamente a la partición 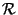 .
A manera de ejemplos, citemos a las relaciones siguientes en un conjunto
.
A manera de ejemplos, citemos a las relaciones siguientes en un conjunto
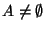 :
:
- Discreta.
- Sea R=(=) la relación que coincide con la identidad en A:
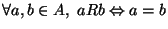 .
Entonces, para toda a, la clase de equivalencia [a] es la mónada cuyo único elemento es a, y el cociente A/R se identifica con A. En este caso, la proyección canónica
.
Entonces, para toda a, la clase de equivalencia [a] es la mónada cuyo único elemento es a, y el cociente A/R se identifica con A. En este caso, la proyección canónica 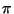 ``es'' la función identidad.
``es'' la función identidad.
- Tosca.
- Sea R=A2 la relación que identifica a cualesquiera dos elementos en A. La única clase de equivalencia es A2 y la proyección canónica
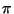 es una función constante.
es una función constante.
Una manera de introducir relaciones de equivalencia en un conjunto es transportando, mediante funciones, las definidas en otros conjuntos. Si S es una relación de equivalencia en un conjunto B y
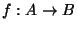 es una función con dominio en un conjunto A y contradominio en el conjunto B entonces la relación R en A definida como
es una función con dominio en un conjunto A y contradominio en el conjunto B entonces la relación R en A definida como
es también una relación de equivalencia.
Si S es la identidad en B, entonces diremos que R es el núcleo de la función f, y lo denotaremos
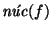 .
Así pues
.
Así pues
Ejemplo. Consideremos a 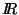 con la identidad y sea
con la identidad y sea
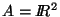 .
La función
.
La función
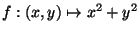 tiene como gráfica a un paraboloide de revolución con vértice en el origen. El núcleo de f consta de todas las parejas de puntos equidistantes al origen, y esta relación de equivalencia determina como espacio cociente a la colección de todos los círculos concéntricos con centro en el origen. Para cada punto
tiene como gráfica a un paraboloide de revolución con vértice en el origen. El núcleo de f consta de todas las parejas de puntos equidistantes al origen, y esta relación de equivalencia determina como espacio cociente a la colección de todos los círculos concéntricos con centro en el origen. Para cada punto
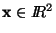 ,
su clase de equivalencia es el círculo que pasa por él y tiene centro en el origen. El índice de la relación de equivalencia es infinito y coincide con la cardinalidad de
,
su clase de equivalencia es el círculo que pasa por él y tiene centro en el origen. El índice de la relación de equivalencia es infinito y coincide con la cardinalidad de 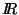 .
.
Supongamos ahora que (A,*,u) es un monoide. Una relación de equivalencia R en A se dice ser una congruencia si se cumple lo siguiente:
es decir, si ``factores equivalentes dan productos equivalentes''.
Proposición 2.8
Sean
(
S1,*
1,
u1) y
(
S2,*
2,
u2) dos monoides y sea
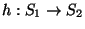
un homomorfismo. Entonces
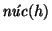
es una congruencia en
S1.
En efecto, supongamos que
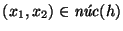 y
y
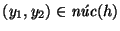 .
Hemos de probar que los respectivos productos coinciden, es decir, que
.
Hemos de probar que los respectivos productos coinciden, es decir, que
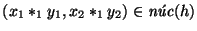 .
Pero esto es inmediato pues
.
Pero esto es inmediato pues
h(x1*1y1)=h(x1)*2h(y1)=h(x2)*2h(y2)=h(x2*1y2).
Observación 2.2
Si (S,*,u) es un monoide y R es una congruencia en S, entonces podemos ``calcar'' la operación * de S en una nueva operación en el cociente S/R de manera que este cociente sea un monoide y la proyección canónica un homomorfismo.
En efecto, para cualesquiera dos clases de equivalencia
[a]R,[b]R definamos
[a]R*S/R[b]R=[a*b]R. Observamos inmediatamente que
- 1.
- la definición de la operación *S/R no depende de los representantes que se elija en las clases
[a]R,[b]R pues R es una congruencia:
- 2.
- la clase de equivalencia de u, [u]R, es la unidad en el cociente S/R, y
- 3.
- la definición
[a]R*S/R[b]R=[a*b]R puede ser reescrita como
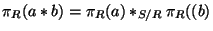 ,
lo que a su vez indica que la proyección canónica es, efectivamente, un homomorfismo.
,
lo que a su vez indica que la proyección canónica es, efectivamente, un homomorfismo.
Ejemplos.
1. Se vió que
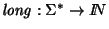 es un homomorfismo. Dos palabras están en el núcleo de
es un homomorfismo. Dos palabras están en el núcleo de
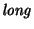 ,
llamémoslo R, si y sólo si son de igual longitud. Por tanto, para cada palabra
,
llamémoslo R, si y sólo si son de igual longitud. Por tanto, para cada palabra  su clase de equivalencia
su clase de equivalencia
![$[\sigma]_R$](img290.gif) es el conjunto de palabras que tienen la misma longitud que
es el conjunto de palabras que tienen la misma longitud que 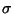 .
Si
.
Si
 entonces podemos identificar a la clase
entonces podemos identificar a la clase
![$[\sigma]_R$](img290.gif) con el número n.
Para dos palabras
con el número n.
Para dos palabras
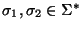 ,
con
,
con
 y
y
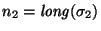 ,
tenemos que
,
tenemos que
es decir, la operación que induce la congruencia coincide con la suma usual de  .
Así pues, podemos identificar naturalmente al monoide
.
Así pues, podemos identificar naturalmente al monoide
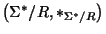 con el monoide
con el monoide
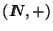 .
.
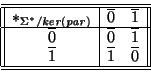
2. La función de paridad
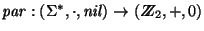 es un homomorfismo. Una pareja de palabras está en el núcleo de
es un homomorfismo. Una pareja de palabras está en el núcleo de
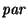 si y sólo si sus dos componentes son de igual paridad: O bien ambas son de longitud par, o bien ambas son de longitud impar. Escribamos
si y sólo si sus dos componentes son de igual paridad: O bien ambas son de longitud par, o bien ambas son de longitud impar. Escribamos
Entonces
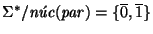 ,
por lo que
,
por lo que
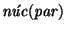 es de índice 2, y la operación que induce la concatenación es, precisamente
es de índice 2, y la operación que induce la concatenación es, precisamente
Así, se identifica
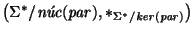 con el monoide
con el monoide
 .
.
3. Sea n>0 y sea
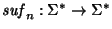 el homomorfismo que trunca una palabra para quedarse con el sufijo de longitud a los sumo n.
Una pareja de palabras estará en el núcleo de
el homomorfismo que trunca una palabra para quedarse con el sufijo de longitud a los sumo n.
Una pareja de palabras estará en el núcleo de
 sólo si ambas palabras poseen un sufijo común de longitud a lo más n. Así pues hay
sólo si ambas palabras poseen un sufijo común de longitud a lo más n. Así pues hay
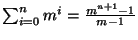 clases de equivalencia para la relación
clases de equivalencia para la relación
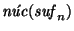 ,
donde m es el número de símbolos en el alfabeto
,
donde m es el número de símbolos en el alfabeto 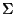 .
La operación que induce la concatenación en el cociente
.
La operación que induce la concatenación en el cociente
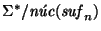 coincide con la operación definida en el monoide
coincide con la operación definida en el monoide
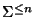 :
Dadas dos palabras, las concatena primero y luego toma el sufijo de longitud n.
:
Dadas dos palabras, las concatena primero y luego toma el sufijo de longitud n.
 se identifica así con el monoide
se identifica así con el monoide
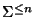 .
.
Sean
(S1,*1,u1) y
(S2,*2,u2) dos monoides y sea
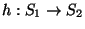 un homomorfismo. h se dice ser
un homomorfismo. h se dice ser
- un monomorfismo si h es inyectiva, es decir, si
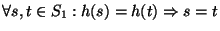 ,
,
- un epimorfismo si h es suprayectiva, es decir, si
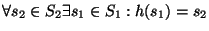 ,
y
,
y
- un isomorfismo si h es a la vez un monomorfismo y un epimorfismo.
La imagen de un homomorfismo
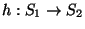 es
es
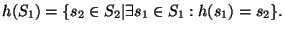 Escribiremos
Escribiremos
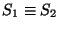 para denotar el hecho de que los monoides S1 y S2 son isomorfos, es decir, de que existe un isomorfismo
para denotar el hecho de que los monoides S1 y S2 son isomorfos, es decir, de que existe un isomorfismo
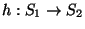 .
.
Observación 2.3
Las siguientes relaciones se siguen inmediatamente para un homomorfismo
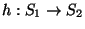
:
- 1.
- h(S1) es un submonoide de S2.
- 2.
- h es un monomorfismo si y sólo si
 ,
es decir, el núcleo de h coincide con la identidad.
,
es decir, el núcleo de h coincide con la identidad.
- 3.
- h es un epimorfismo si y sólo si
S2=h(S1)
Teorema 2.4 (del homomorfismo.)
Para cualquier epimorfismo
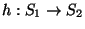
se tiene
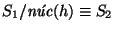
.
En efecto, siendo h un homomorfismo, se tiene que
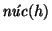 es una congruencia. Por tanto, el cociente
es una congruencia. Por tanto, el cociente
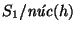 posee una estructura de monoide. Consideremos la función
posee una estructura de monoide. Consideremos la función
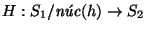 ,
,
![$[s]\mapsto h(s)$](img317.gif) .
Es claro que H está bien definida (es decir, H([s]) no depende del representante que se tome para la clase [s]), y que es un isomorfismo.
.
Es claro que H está bien definida (es decir, H([s]) no depende del representante que se tome para la clase [s]), y que es un isomorfismo.
Ejemplo. Sea 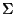 un alfabeto y sea
un alfabeto y sea
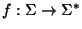 una función de sustitución. Sea
una función de sustitución. Sea
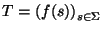 el conjunto de palabras correspondientes a símbolos de
el conjunto de palabras correspondientes a símbolos de 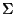 mediante la función f. Sea
mediante la función f. Sea
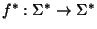 el homomorfismo que extiende a f. Entonces
el homomorfismo que extiende a f. Entonces
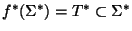 .
Ahora, una pareja
.
Ahora, una pareja
 está en el núcleo de f* si y sólo si bajo f* ambas se convierten en una misma palabra de T*. De acuerdo con el Primer Teorema Fundamental de Homomorfismos se tiene
está en el núcleo de f* si y sólo si bajo f* ambas se convierten en una misma palabra de T*. De acuerdo con el Primer Teorema Fundamental de Homomorfismos se tiene
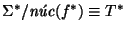 .
.



Siguiente: Propiedades de lenguajes
Un nivel arriba: Monoide de cadenas
Anterior: Homomorfismos
Guillermo Morales-Luna
2000-06-27
![\begin{eqnarray*}[a]_R\not=[b]_R &\Rightarrow& [a]_R\cap[b]_R=\emptyset \\
\forall b\in A\;\exists a\in A &:& b\in [a]_R
\end{eqnarray*}](img263.gif)