



Siguiente: Algunas variantes
Un nivel arriba: Particiones en base a
Anterior: Particiones en base a
Sea 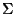 un alfabeto. Construimos en esta sección una relación de congruencia lateral en
un alfabeto. Construimos en esta sección una relación de congruencia lateral en 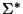 que utilizaremos frecuentemente en este curso.
Sea L un lenguaje de
que utilizaremos frecuentemente en este curso.
Sea L un lenguaje de 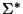 .
La relación RL que induce el lenguaje L se define como sigue:
.
La relación RL que induce el lenguaje L se define como sigue:
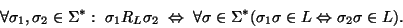 |
(1) |
Es decir, dos palabras están relacionada según RL si y sólo si, al añadírseles un mismo sufijo, o bien ambas palabras resultantes quedan en el lenguaje, o bien ambas dejan de pertenecer al lenguaje.
Es fácil ver que RL es una relación de equivalencia. De hecho, es una congruencia derecha pues rige la implicación:
El índice del lenguaje L es, por definición, el índice de la relación RL.
La noción de índice es de particular importancia para analizar la complejidad del lenguaje.
El Teorema de Myhill-Nerode, que veremos más adelante, asevera que un lenguaje será regular si y sólo si es de índice finito.
Guillermo Morales-Luna
2000-06-27