



Siguiente: Ejemplos de gramáticas
Un nivel arriba: Gramáticas formales
Anterior: Gramáticas formales
Una gramática es una estructura
G=(V,T, P, s0) donde
Una pareja
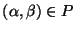 se escribe como
se escribe como
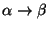 ,
o bien
,
o bien
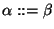 .
Se dice que
.
Se dice que 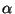 es el antecedente de la regla y que
es el antecedente de la regla y que 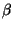 es su consecuente. Si
es su consecuente. Si
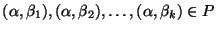 es un conjunto de reglas con un antecedente común, se simplifica la notación y se escribe
es un conjunto de reglas con un antecedente común, se simplifica la notación y se escribe
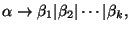 o alternativamente
o alternativamente
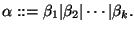 Dadas dos palabras
Dadas dos palabras
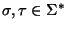 decimos que
decimos que 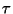 se sigue de
se sigue de  en G, y escribimos
en G, y escribimos
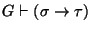 ,
o simplemente
,
o simplemente
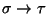 ,
cuando
,
cuando 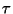 resulte de
resulte de  al intercambiar una partícula de
al intercambiar una partícula de  ,
que sea el antecedente de una regla, por el respectivo consecuente de la regla. En símbolos,
,
que sea el antecedente de una regla, por el respectivo consecuente de la regla. En símbolos,
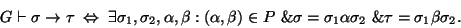 |
(3) |
Decimos que 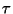 se deriva de
se deriva de  en G, y escribimos
en G, y escribimos
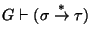 ,
o simplemente
,
o simplemente
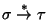 ,
si existe una sucesión finita de palabras, cuyos primero y último elementos coinciden con
,
si existe una sucesión finita de palabras, cuyos primero y último elementos coinciden con  y
y 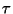 respectivamente, y cualquier elemento en la sucesión se sigue del anterior. En símbolos,
respectivamente, y cualquier elemento en la sucesión se sigue del anterior. En símbolos,
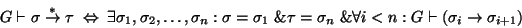 |
(4) |
En tal caso, la sucesión de palabras y producciones
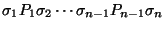 ,
donde
,
donde
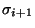 se sigue de
se sigue de
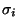 precisamente por la aplicación de la producción Pi, es una derivación de
precisamente por la aplicación de la producción Pi, es una derivación de 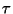 a partir de
a partir de  .
Así pues, la relación ``se_deriva'' es la cerradura reflexivo-transitiva de la relación ``se_sigue''
El lenguaje de la gramática es el conjunto de palabras formadas con símbolos terminales que se derivan del símbolo inicial,
.
Así pues, la relación ``se_deriva'' es la cerradura reflexivo-transitiva de la relación ``se_sigue''
El lenguaje de la gramática es el conjunto de palabras formadas con símbolos terminales que se derivan del símbolo inicial,




Siguiente: Ejemplos de gramáticas
Un nivel arriba: Gramáticas formales
Anterior: Gramáticas formales
Guillermo Morales-Luna
2000-06-27
![\begin{eqnarray*}V &:& \mbox{\rm\begin{minipage}[t]{38em}
es un conjunto de s\'...
...em producciones} o {\em reglas sint\'acticas}.
\end{minipage}}
\end{eqnarray*}](img398.gif)
![\begin{eqnarray*}V &:& \mbox{\rm\begin{minipage}[t]{38em}
es un conjunto de s\'...
...em producciones} o {\em reglas sint\'acticas}.
\end{minipage}}
\end{eqnarray*}](img398.gif)