Observación 2.3
Los autómatas
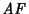
y
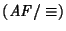
son equivalentes si y sólo si el conjunto de estados finales
F es la unión de algunas clases de equivalencia respecto a ``
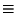
''.
Teorema 2.2 (de homomorfismo de autómatas)
Si
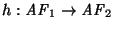
es un epimorfismo de autómatas tal que
F1 es la unión de clases de equivalencia respecto a
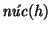
,
entonces el cociente
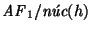
es isomorfo a
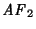
.
En símbolos,
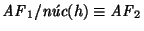
.
![\begin{eqnarray*}Q/\equiv &:& \mbox{\rm estados,} \\
\mbox{\it tran\/}':([q],e...
...\rm transici\'on,} \\
{[q_0]} &:& \mbox{\rm estado inicial.}
\end{eqnarray*}](img905.gif)