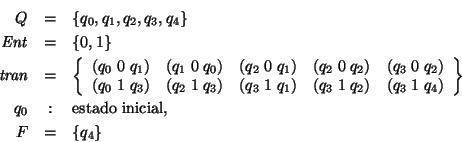Siguiente: Representación de transiciones mediante
Un nivel arriba: Autómatas no-deterministas
Anterior: Autómatas no-deterministas
Los autómatas no-deterministas se conforman como los autómatas finitos ya vistos, salvo que sus transiciones, en lugar de ser funciones, son relaciones que a cada pareja (estado,estímulo) le asocian varios, uno o ningún estado. Más precisamente:
Un semiautómata no-determinista es una estructura de la forma
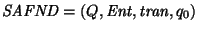 donde
donde
Un autómata no-determinista es una pareja
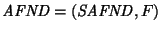 donde SAFND es un semiautómata no-determinista y
donde SAFND es un semiautómata no-determinista y
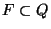 es un conjunto de estados finales.
Si
es un conjunto de estados finales.
Si
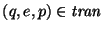 decimos que se puede transitar a p desde el estado q cuando arriba un símbolo e. Para cada pareja
decimos que se puede transitar a p desde el estado q cuando arriba un símbolo e. Para cada pareja
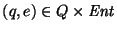 su imagen bajo la transición es el conjunto
su imagen bajo la transición es el conjunto
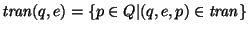 ,
es decir, es el conjunto de estados a los que se puede transitar desde q con e.
De manera reiterada, para
,
es decir, es el conjunto de estados a los que se puede transitar desde q con e.
De manera reiterada, para
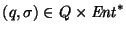 ,
definimos la imagen
,
definimos la imagen
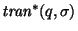 como sigue:
como sigue:
Para cada
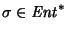 definimos
definimos
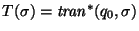 .
Una palabra
.
Una palabra
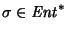 es reconocida por el autómata
es reconocida por el autómata
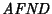 si algún estado en
si algún estado en 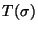 es final. El lenguaje del autómata
es final. El lenguaje del autómata
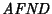 consiste de todas las palabras que reconoce,
consiste de todas las palabras que reconoce,
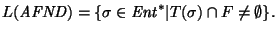
Ejemplo. Sea
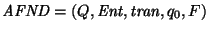 el autómata no-determinista tal que
el autómata no-determinista tal que
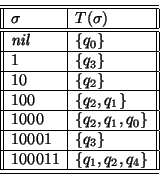
En la siguiente tabla presentamos el cálculo de la correspondiente función T en algunas palabras:
Así pues,
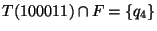 y consecuentemente
y consecuentemente
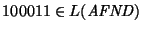 .
.
Observación 3.1
Todo autómata finito (determinista) es también un autómata finito no-determinista.
En efecto, las funciones son casos particulares de relaciones. Por tanto, toda función de transición, es una relación de transición.




Siguiente: Representación de transiciones mediante
Un nivel arriba: Autómatas no-deterministas
Anterior: Autómatas no-deterministas
Guillermo Morales-Luna
2000-06-27