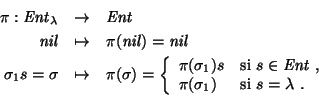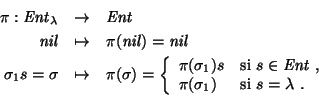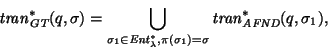Siguiente: Supresión de transiciones vacías
Un nivel arriba: Gráficas de transición
Anterior: Gráficas de transición
Sea
 un alfabeto finito y sea
un alfabeto finito y sea 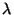 un símbolo que no esté en
un símbolo que no esté en
 .
Sea
.
Sea
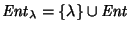 la extensión, mediante la añadidura del símbolo
la extensión, mediante la añadidura del símbolo 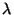 ,
del alfabeto dado.
Naturalmente, el diccionario
,
del alfabeto dado.
Naturalmente, el diccionario
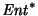 está incluido en el diccionario
está incluido en el diccionario
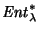 .
Por otro lado, sea
.
Por otro lado, sea
la transformación que en cada palabra de
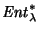 suprime todas las apariciones del símbolo
suprime todas las apariciones del símbolo 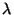 .
Acaso vale la pena decir aquí que
.
Acaso vale la pena decir aquí que 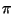 es el homomorfismo entre diccionarios que extiende a las sustitución
es el homomorfismo entre diccionarios que extiende a las sustitución
Una gráfica de transición sobre el alfabeto
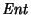 es una estructura
es una estructura
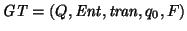 que coincide con un autómata no-determinista
que coincide con un autómata no-determinista
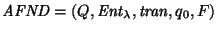 sobre el alfabeto
sobre el alfabeto
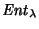 .
Se dice que todas las transiciones de la forma
.
Se dice que todas las transiciones de la forma
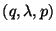 son transiciones-
son transiciones-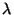 ,
o transiciones-vacías.
Para cualquier estado
,
o transiciones-vacías.
Para cualquier estado 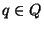 y cualquier palabra
y cualquier palabra
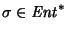 el conjunto de estados accesibles por
el conjunto de estados accesibles por  desde q en
desde q en
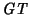 es
es
es decir, un estado es accesible si hay una sucesión de transiciones, que puede incluir transiciones-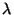 ,
correspondiente a los símbolos de
,
correspondiente a los símbolos de  desde el estado q hasta ese estado.
Introduzcamos también en este caso, la siguiente relación en
desde el estado q hasta ese estado.
Introduzcamos también en este caso, la siguiente relación en
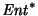 :
:
Como antes, se tiene que
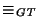 es una relación de equivalencia congruente con la concatenación. Por tanto, el cociente
es una relación de equivalencia congruente con la concatenación. Por tanto, el cociente
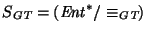 es un monoide, dicho de la gráfica de transición.
es un monoide, dicho de la gráfica de transición.




Siguiente: Supresión de transiciones vacías
Un nivel arriba: Gráficas de transición
Anterior: Gráficas de transición
Guillermo Morales-Luna
2000-06-27