Siguiente: Expresiones regulares
Un nivel arriba: Autómatas finitos y expresiones
Anterior: Propiedades de cerradura
1. Construya máquinas de Mealy y de Moore con el desempeño siguiente: Para entradas en (0+1)*, si la entrada termina con el sufijo 101 emite A; si la entrada termina con el sufijo 110 emite B; en otro caso emite C.
2. Construya máquinas de Mealy y de Moore con el desempeño siguiente: Para entradas en (0+1+2)*, escribe el residuo en base 5 del número que, en base 3 está dado por la entrada.
3. Sea
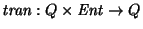 la función de transición de un autómata finito. Demuestre que para cada
la función de transición de un autómata finito. Demuestre que para cada 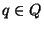 y cada
y cada
 se tiene
se tiene
4. Construya un autómata finito sobre el alfabeto
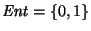 que reconozca al lenguaje consistente de las cadenas de caracteres con tres 0's consecutivos.
que reconozca al lenguaje consistente de las cadenas de caracteres con tres 0's consecutivos.
5. Construya un autómata finito sobre el alfabeto
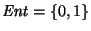 que reconozca al lenguaje consistente de las cadenas de caracteres tales que cada bloque de cinco caracteres consecutivos contiene al menos dos 0's.
que reconozca al lenguaje consistente de las cadenas de caracteres tales que cada bloque de cinco caracteres consecutivos contiene al menos dos 0's.
6. Construya un autómata finito sobre el alfabeto
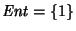 que reconozca al lenguaje
que reconozca al lenguaje
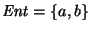 .
.
7. Construya un autómata finito sobre el alfabeto
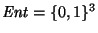 que reconozca al conjunto de palabras cuyos cuatro últimos símbolos forman la partícula bbab.
que reconozca al conjunto de palabras cuyos cuatro últimos símbolos forman la partícula bbab.
8. Construya un autómata finito sobre el alfabeto
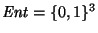 que reconozca al conjunto de palabras cuyos cinco últimos símbolos incluyen dos a's y tres b's.
que reconozca al conjunto de palabras cuyos cinco últimos símbolos incluyen dos a's y tres b's.
9. Revisor de sumas binarias: Construya un autómata finito sobre el alfabeto
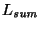 que reconozca al lenguaje
que reconozca al lenguaje
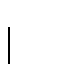 tal que
tal que
Así, por ejemplo, como 6+14=20 se tiene
10. Construya un autómata finito sobre el alfabeto
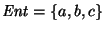 que reconozca al lenguaje consistente de los palíndromas de longitud a lo sumo 6.
que reconozca al lenguaje consistente de los palíndromas de longitud a lo sumo 6.
11. Construya un autómata finito sobre el alfabeto
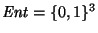 que reconozca al lenguaje consistente de las palabras cuyo antepenúltimo símbolo es b.
que reconozca al lenguaje consistente de las palabras cuyo antepenúltimo símbolo es b.
12. Demuestre que el autómata cuya transición es
y tiene a q0 como estado inicial y a él mismo como único estado final, reconoce a todas las cadenas con un mismo número de 0's y 1's que además son tales que cualquier prefijo posee a lo más un 1 más que 0's o bien a lo más un 0 más que 1's.
13. Construya un autómata no-determinista sobre el alfabeto
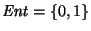 que reconozca al lenguaje consistente de las cadenas de caracteres tales que dos 0's están separados por 4i caracteres, para algún
que reconozca al lenguaje consistente de las cadenas de caracteres tales que dos 0's están separados por 4i caracteres, para algún 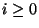 .
.
14. Construya un autómata no-determinista sobre el alfabeto
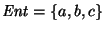 que reconozca al lenguaje consistente de las cadenas de caracteres tales que dan el mismo valor evaluadas de derecha a izquierda o de izquierda a derecha según la operación (no-asociativa) siguiente:
que reconozca al lenguaje consistente de las cadenas de caracteres tales que dan el mismo valor evaluadas de derecha a izquierda o de izquierda a derecha según la operación (no-asociativa) siguiente:
15. Construya un autómata no-determinista sobre el alfabeto
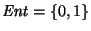 que reconozca al lenguaje consistente de las cadenas de caracteres tales que el décimo símbolo, contado desde la derecha, es un 1.
que reconozca al lenguaje consistente de las cadenas de caracteres tales que el décimo símbolo, contado desde la derecha, es un 1.
16. Pruebe que para todo autómata no-determinista A existe un autómata no-determinista B con un único estado final tal que bien L(B)=L(A) o bien
 .
.
17. a) Construya un autómata finito determinista equivalente al autómata no-determinista cuyo estado inicial es q0, su único estado final es q3 y cuya tabla de transición es la siguiente:
b) Construya un autómata finito determinista equivalente al autómata no-determinista cuyo estado inicial es q0, sus estados finales son q1,q3 y cuya tabla de transición es la siguiente:
18. Construya un autómata finito determinista equivalente al autómata bidireccional cuyo estado inicial es q0, su estado final es q2 y cuya tabla de transición es la siguiente:
19. Un autómata bidireccional no-determinista se define de manera similar a uno bidireccional determinista con la salvedad de que para cada pareja (estado_actual, símbolo_leído) se tiene un conjunto de posibles movimientos. Pruebe que todo autómata bidireccional no-determinista es equivalente a un autómata finito determinista.
Sug. La observación de que ningún estado puede repetirse con la misma dirección en una sucesión de cruce ya no es válida en esta caso. Sin embargo, para cada cadena aceptada puede considerarse la computación más corta que conduce a reconocimiento.
20. Muestre que al permitir que en los autómatas bidireccionales no-deterministas la cabeza lectora permanezca inmóvil aún cuando haya cambios de estados ``no se incrementa la computabilidad'', es decir, todo tal autómata bidireccional es equivalente a uno finito determinista.




Siguiente: Expresiones regulares
Un nivel arriba: Autómatas finitos y expresiones
Anterior: Propiedades de cerradura
Guillermo Morales-Luna
2000-06-27
 se tiene
se tiene
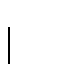 tal que
tal que
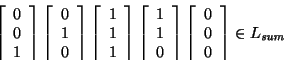
![\begin{displaymath}\left[\begin{array}{c}
0 \\ 0 \\ 1
\end{array}\right]
\lef...
...\\ 0 \\ 0
\end{array}\right] \in L_{\mbox{\scriptsize\it sum}}\end{displaymath}](img1195.gif)

 .
.