



Siguiente: El mundo de los
Un nivel arriba: Expresiones regulares y sistemas
Anterior: Expresiones regulares y sistemas
Los Sistemas de Planeación generan automáticamente
procedimientos para resolver problemas bien planteados. En ellos ,
se describe al Universo del Problema, el cual consiste de sus
objetos y de las relaciones entre ellos. Se describe también a
las acciones legales, o movimientos. Cada una de ellas involucra a
un conjunto de precondiciones que se deben de cumplir para aplicar
la acción, y otro de postcondiciones que se cumplirán tras
haber aplicado la acción. Una acción sólo se aplica a
algunos estados, y al hacerlo, los transforma en otros nuevos. Si
la acción a se puede aplicar al estado e escribiremos
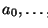 y
denotaremos por a( e ) al estado que se obtiene de e al aplicar a.
Una acción a1 es sucesiva de otra a0 respecto al estado e si se
cumple que
y
denotaremos por a( e ) al estado que se obtiene de e al aplicar a.
Una acción a1 es sucesiva de otra a0 respecto al estado e si se
cumple que
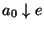 .
Un plan, aplicado a un estado e, es una
sucesión de acciones
.
Un plan, aplicado a un estado e, es una
sucesión de acciones
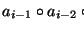 tal que
tal que
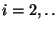 ,
a1 es sucesiva de
a0 respecto a e y además ai+1 es sucesiva de ai respecto a
,
a1 es sucesiva de
a0 respecto a e y además ai+1 es sucesiva de ai respecto a
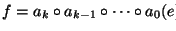 ,
,
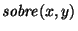 .
El problema de cualquier Sistema de Planeación consiste en
encontrar, para un estado inicial e y uno meta f dados, un plan
.
El problema de cualquier Sistema de Planeación consiste en
encontrar, para un estado inicial e y uno meta f dados, un plan
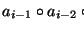 tal que
tal que
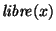 ,
siempre que exista un tal plan, o bien indicar que no existe, en otro caso.
El Problema de los Bloques tiene como
universo a un conjunto de n+1 objetos, de los cuales n son bloques
y el último es el piso. Como relaciones sólo tiene a dos:
,
siempre que exista un tal plan, o bien indicar que no existe, en otro caso.
El Problema de los Bloques tiene como
universo a un conjunto de n+1 objetos, de los cuales n son bloques
y el último es el piso. Como relaciones sólo tiene a dos:
-
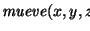 ``el bloque x está sobre el objeto y'', y
``el bloque x está sobre el objeto y'', y
-
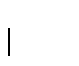 ''el objeto x está libre para recibir un bloque encima de él''.
''el objeto x está libre para recibir un bloque encima de él''.
Las acciones legales son instancias de
 ``mueve el bloque x del objeto y al objeto z'', con
``mueve el bloque x del objeto y al objeto z'', con
- precondiciones:
y
- postcondiciones:
Cada estado se especifica como una
conjunción de enunciados atómicos, o átomos, los cuales son
instancias de relaciones con objetos.
Un primer criterio para generar planes de manera automática
es poner a los átomos de una meta en una lista,
considerarlos como ``submetas'', e ir lográndolos uno a uno. Es
necesario preservar lo logrado al tratar de lograr un nuevo
átomo. Si acaso no fuera posible, se permuta a la lista de
átomos y se repite el proceso.
A veces este criterio no logra estados metas, aún cuando efectivamente fueren alcanzables. La anomalía de Sussman es un ejemplo: Con
tres bloques 1, 2 , 3, estado inicial
y meta
la estrategia anterior no logra
encontrar un plan. En cualquiera de las dos permutaciones de la meta uno se ve obligado a deshacer logros ya obtenidos.
El problema de planeación ha sido tratado con diversos enfoques, basados, en general, en deducción
automática. Alternativamente, consideraremos aquí
un enfoque de tipo combinatorio. Veremos que es posible calcular
no sólo una solución, sino a todas las existentes. Primeramente, calcularemos el número de estados en el
Problema de Bloques (PB). Presentamos luego una solución del correspondiente problema de planeación con técnicas de
autómatas finitos. Finalmente observamos que, bien que el PB (de
hecho cualquier otro problema para los Sistemas de Planeación), se resuelve por completo con estas técnicas, los
algoritmos utilizados son tan complejos que aún queda lejos su
implementación práctica.




Siguiente: El mundo de los
Un nivel arriba: Expresiones regulares y sistemas
Anterior: Expresiones regulares y sistemas
Guillermo Morales-Luna
2000-06-27
 ''el objeto x está libre para recibir un bloque encima de él''.
''el objeto x está libre para recibir un bloque encima de él''.
 ''el objeto x está libre para recibir un bloque encima de él''.
''el objeto x está libre para recibir un bloque encima de él''.
 ``mueve el bloque x del objeto y al objeto z'', con
``mueve el bloque x del objeto y al objeto z'', con