



Siguiente: Autómatas de pila
Un nivel arriba: Expresiones regulares
Anterior: Ejercicios
1. Máquinas de Mealy como ``traductores'': Recordamos que una máquina de Mealy es una estructura de la forma
donde, para fines de este ejercicio:
Escriba un programa que reciba como entrada los números enteros n,m,M y los arreglos
 y
y
 .
Posteriormente, para cada cadena
.
Posteriormente, para cada cadena
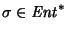 dada, ha de calcular la cadena de respuesta
dada, ha de calcular la cadena de respuesta
 .
.
2. Máquinas de Moore como ``traductores'': Recordamos que una máquina de Moore es una estructura de la forma
donde, para fines de este ejercicio:
Escriba un programa que reciba como entrada los números enteros n,m,M y los arreglos
 y
y
 .
Posteriormente, para cada cadena
.
Posteriormente, para cada cadena
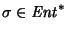 dada, ha de calcular la cadena de respuesta
dada, ha de calcular la cadena de respuesta
 .
.
3. Equivalencia entre máquinas de Mealy y de Moore: Escriba un programa que dada una máquina de Mealy, en la representación descrita para el programa 1 de esta lista, calcule la máquina de Moore equivalente, tal que todos sus estados sean accesibles, y la exprese en la representación descrita para el programa 2 de esta lista.
4. Indistinguibilidad en máquinas de Moore:
- 1.
- Dada una máquina de Moore M, dos estados qi,qj son indistiguibles si para cualquier palabra
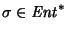 las respuestas de los estados a los que se llega con
las respuestas de los estados a los que se llega con  ,
partiendo de qi y de qj, coinciden. Esta es una relación de equivalencia entre estados.
Escriba un programa que dada una máquina de Moore M calcule al cociente
,
partiendo de qi y de qj, coinciden. Esta es una relación de equivalencia entre estados.
Escriba un programa que dada una máquina de Moore M calcule al cociente
 .
.
- 2.
- Dada una máquina de Moore M, dos palabras
 son indistiguibles si los estados a los que llegan, partiendo del inicial,
son indistiguibles si los estados a los que llegan, partiendo del inicial,
 y
y
 son indistinguibles. Esta es una relación de equivalencia entre palabras.
Escriba un programa que dada una máquina de Moore M calcule al cociente
son indistinguibles. Esta es una relación de equivalencia entre palabras.
Escriba un programa que dada una máquina de Moore M calcule al cociente
 .
.
- 3.
- ¿Qué relación hay entre los cocientes encontrados para una misma máquina?
Nota: En lo que sigue, un semiautómata de n estados con m símbolos se representará como una matriz S del tipo
![$[\![1,n]\!]^{m\times n}$](img1636.gif) ,
con la intención obvia de que
,
con la intención obvia de que
 es el índice del estado al que se llega desde el estado j cuando se aplica el símbolo i.
Un autómata se representará como una pereja (S,F), donde
es el índice del estado al que se llega desde el estado j cuando se aplica el símbolo i.
Un autómata se representará como una pereja (S,F), donde
![$F\subset[\![1,n]\!]$](img1638.gif) es el conjunto de índices de estados finales.
es el conjunto de índices de estados finales.
5. Parte accesible de un autómata finito: Dado un autómata, calcule la parte accesible del autómata, y renombre, si fuera necesario, al conjunto de estados resultante para expresarlo con la convención que aquí hemos adoptado para representar autómatas.
6. Homomorfismos de autómatas: Escriba un programa que dados dos autómatas decida si hay un homomorfismo del primer autómata al segundo.
Si
 fuese un homomorfismo entre dos autómatas, diga que dos estados
qi1,qj1 son equivalentes si
h(qi1)=h(qj1). Esta es, en efecto, una relación de equivalencia. Calcule sus clases de equivalencia.
fuese un homomorfismo entre dos autómatas, diga que dos estados
qi1,qj1 son equivalentes si
h(qi1)=h(qj1). Esta es, en efecto, una relación de equivalencia. Calcule sus clases de equivalencia.
7. Monoides de autómatas deterministas: Escriba un programa que reciba un autómata determinista y calcule la tabla de multiplicación de su monoide. (Cfr. Sec. 4.2.2 de las ``Notas del Curso'').
8. Acciones de grupos libres en monoides: Suponga dado un monoide
![$M\in [\![1,n]\!]^{n\times n}$](img583.gif) ,
por su tabla de multiplicación, con unidad, digamos u=1. Para un conjunto no-vacío de elementos
,
por su tabla de multiplicación, con unidad, digamos u=1. Para un conjunto no-vacío de elementos
![$I\subset [\![1,n]\!]$](img1640.gif) denotamos por [I]M al mínimo submonoide, del monoide M, que contiene al conjunto I. [I]M es el submonoide generado por I en M.
Si I consta de un único elemento, digamos
denotamos por [I]M al mínimo submonoide, del monoide M, que contiene al conjunto I. [I]M es el submonoide generado por I en M.
Si I consta de un único elemento, digamos  ,
,
 ,
el submonoide [I]M se calcula como sigue:
,
el submonoide [I]M se calcula como sigue:
- 1.
- Inicialmente hágase
![$[I]_M=\{1\}=\{a^0\}$](img1643.gif) ,
y
,
y
 .
.
- 2.
- Mientras que
 ,
sáquese el primer elemento x, digamos x=ai, que quede en
,
sáquese el primer elemento x, digamos x=ai, que quede en
 y añádasele a [I]M. Tómese ahora
y añádasele a [I]M. Tómese ahora
 .
Si y no aparece aún en [I]M colóquese y en la lista
.
Si y no aparece aún en [I]M colóquese y en la lista
 .
.
- 3.
- Cuando no queden elementos por probar, el submonoide generado por a queda en [I]M y a partir de ahí es posible construir la tabla de multiplicación de
![$[\{a\}]_M$](img1648.gif) .
.
Si I consta de más de un elemento, digamos
 ,
,
 ,
el submonoide [I]M se calcula como sigue:
,
el submonoide [I]M se calcula como sigue:
- 1.
- Inicialmente hágase
![$[I]_M=[\{a_1\ldots,a_{k-1}\}]_M$](img1651.gif) ,
el submonoide generado por los primeros k-1 elementos, y
,
el submonoide generado por los primeros k-1 elementos, y
 .
.
- 2.
- Mientras que
 ,
sáquese el primer elemento x, que quede en
,
sáquese el primer elemento x, que quede en
 .
Si acaso ya estuviese en [I]M termínese el proceso sin más. En otro caso, añádasele a [I]M y para cada elemento z en [I]M, tómese
.
Si acaso ya estuviese en [I]M termínese el proceso sin más. En otro caso, añádasele a [I]M y para cada elemento z en [I]M, tómese
 e
e
 .
Si
.
Si
 no aparece ni en [I]M ni en
no aparece ni en [I]M ni en
 ,
colóquese
,
colóquese
 en la lista
en la lista
 .
Si
.
Si
 no aparece ni en [I]M ni en
no aparece ni en [I]M ni en
 ,
colóquese
,
colóquese
 en la lista
en la lista
 .
.
- 3.
- Cuando no queden elementos por probar, el submonoide generado por I queda en [I]M y a partir de ahí es posible construir la tabla de multiplicación de [I]M.
Escriba un programa que dado un monoide en M encuentre un conjunto mínimo de elementos
 tal que M=[I]M.
tal que M=[I]M.
9. Autómatas de máximos monoides: (Este programa se ha de apoyar de manera esencial en el programa anterior en esta lista.) Dado n considere un conjunto Q de n estados, para fijar ideas,
![$Q=[\![1,n]\!]$](img1657.gif) .
Sea
.
Sea
 una enumeración de todas las funciones
una enumeración de todas las funciones  .
.
 es un monoide con la composición de funciones como operación. Sea m=nn y sea An un subconjunto de m símbolos.
Consideremos el semiautómata
es un monoide con la composición de funciones como operación. Sea m=nn y sea An un subconjunto de m símbolos.
Consideremos el semiautómata
 tal que
tal que
 .
Entonces su monoide, naturalmente coincide con
.
Entonces su monoide, naturalmente coincide con
 y posee nn elementos.
Escriba un programa que reduzca el semiautómata
y posee nn elementos.
Escriba un programa que reduzca el semiautómata
 a uno
a uno
 sobre un alfabeto mínimo
sobre un alfabeto mínimo
 tal que el monoide del semiautómata reducido
tal que el monoide del semiautómata reducido
 coincida también con
coincida también con
 .
.
10. Indistinguibilidad de estados en autómatas: Para un autómata
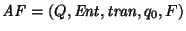 se tiene la relación en Q:
se tiene la relación en Q:
![\begin{displaymath}\forall p,q\in Q:\ \ p\equiv_{\mbox{\scriptsize\it Ind}} q\ \...
... F\ \ \Leftrightarrow\ \ \mbox{\it tran\/}^*(q,\sigma)\in F]
\end{displaymath}](img921.gif) |
(50) |
Escriba un programa que dado un autómata calcule el autómata cociente correspondiente a esta relación.
Extienda este programa para que dado un autómata calcule el mínimo autómata equivalente.
11. Monoides de autómatas no-deterministas: Escriba un programa que reciba un autómata no-determinista y calcule la tabla de multiplicación de su monoide. (Cfr. Sec. 4.3.2 de las ``Notas del Curso'').
12. No-Determinismo = Determinismo: Escriba un programa que reciba un autómata no-determinista o una gráfica de transición y calcule el autómata determinista equivalente al dispositivo dado. (Cfr. Sec. 4.3 y 4.4 de las ``Notas del Curso'').
13. Bidireccionalidad = Monodireccionalidad: Escriba un programa que reciba un autómata bidireccional y calcule el autómata (monodireccional) equivalente al dispositivo dado. (Cfr. Sec. 4.5 de las ``Notas del Curso'').
14. Analizador de expresiones regulares: Escriba un programa que reciba una expresión regular
 ,
calcule una gráfica de transición cuyo lenguaje sea el expresado por X. (Cfr. Sec. 5.2 de las ``Notas del Curso'').
,
calcule una gráfica de transición cuyo lenguaje sea el expresado por X. (Cfr. Sec. 5.2 de las ``Notas del Curso'').
15. Seudoinversión matricial con expresiones regulares: Escriba un programa que reciba una matriz
 ,
con
,
con  ,
y calcule
,
y calcule
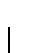 .
(Cfr. Sec. 5.4 de las ``Notas del Curso'').
.
(Cfr. Sec. 5.4 de las ``Notas del Curso'').
16. Caracterización de lenguajes regulares: Utilizando el programa del ejercicio anterior, escriba un programa que reciba un autómata determinista y calcule una expresión regular que represente al lenguaje del autómata. (Cfr. Sec. 5.2 de las ``Notas del Curso'').
17. Reconocedores de lenguajes finitos: Escriba un programa que reciba un conjunto finito de palabras y construya el autómata finito que reconoce únicamente a las palabras dadas.
18. Contención de lenguajes regulares: Escriba un programa que dadas dos expresiones regulares determine si la primera está contenida, y en caso que no, encuentre una palabra en el primer lenguaje que no esté en el segundo.
19. Reconocedor de subpalabras: Escriba un programa que dado un conjunto de k palabras,
 ,
construya una máquina de Moore, con alfabeto de salida
,
construya una máquina de Moore, con alfabeto de salida
![$\left(a_K\right)_{K\subset[\![1,n]\!]}$](img1670.gif) ,
tal que para cualquier palabra dada
,
tal que para cualquier palabra dada 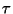 la respuesta del autómata tras de leer
la respuesta del autómata tras de leer 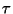 será aK, donde
será aK, donde
 .
.
20. Reconocedor de caminos: Sea G=(V,D), con
 ,
una gráfica dirigida. Una camino es una sucesión de aristas
,
una gráfica dirigida. Una camino es una sucesión de aristas
 tal que
tal que
 .
Escriba un programa que dada una gráfica dirigida, construya un autómata sobre el alfabeto de aristas en la gráfica que reconozca exactamente a los caminos en la gráfica.
.
Escriba un programa que dada una gráfica dirigida, construya un autómata sobre el alfabeto de aristas en la gráfica que reconozca exactamente a los caminos en la gráfica.
21. Reverso de elenguajes regulares: Escriba un programa que dado un autómata finito
 construya el autómata finito
construya el autómata finito
 tal que
tal que
 (reverso del lenguaje reconocido por AF).
(reverso del lenguaje reconocido por AF).
22. Cadenas minimales en lenguajes regulares: Para un lenguaje L sea
el lenguaje consistente de las palabras en L que no poseen prefijo propio en L.
Escriba un programa que dado un autómata finito
 construya el autómata finito
construya el autómata finito
 tal que
tal que
 .
.
23. Cadenas maximales en lenguajes regulares: Para un lenguaje L sea
el lenguaje consistente de las palabras en L que no son prefijo propio de ninguna otra palabra en L.
Escriba un programa que dado un autómata finito
 construya el autómata finito
construya el autómata finito
 tal que
tal que
 .
.
24. Regularidad de estrellas en alfabetos mónicos: Escriba un programa que dado un conjunto finito de índices
 ,
construya un autómata, sobre el alfabeto
,
construya un autómata, sobre el alfabeto  de un único símbolo, que reconozca al lenguaje
de un único símbolo, que reconozca al lenguaje
 .
.
25. Palíndromas de lenguajes regulares: Para un lenguaje L sea
el lenguaje consistente de palíndormas con una ``primera parte'' en L, es decir de palabras, e imágenes especulares, en L.
Escriba un programa que dada una expresión regular E construya el autómata finito
 tal que
tal que
 ,
donde L(E) es el lenguaje expresado por E.
Sugerencia: Razonando por inducción en la construcción de la expresión E, tranfórmela en una expresión que exprese al lenguaje
,
donde L(E) es el lenguaje expresado por E.
Sugerencia: Razonando por inducción en la construcción de la expresión E, tranfórmela en una expresión que exprese al lenguaje
 y a partir de ella construya al autómata pedido.
y a partir de ella construya al autómata pedido.
26. Raíces n-ésimas de lenguajes regulares: Para un lenguaje L y un entero n, sea
el lenguaje consistente de n repeticiones de una ``primera parte'' en L.
Escriba un programa que dada una expresión regular E construya el autómata finito
![$\sqrt[n]{\mbox{\rm AF}}$](img1692.gif) tal que
tal que
![$L(\sqrt[n]{\mbox{\rm AF}})=\sqrt[n]{L(E)}$](img1693.gif) ,
donde L(E) es el lenguaje expresado por E.
Sugerencia: Razonando por inducción en la construcción de la expresión E, transfórmela en una expresión que exprese al lenguaje
,
donde L(E) es el lenguaje expresado por E.
Sugerencia: Razonando por inducción en la construcción de la expresión E, transfórmela en una expresión que exprese al lenguaje
![$\sqrt[n]{L(E)}$](img1694.gif) y a partir de ella construya al autómata pedido.
y a partir de ella construya al autómata pedido.
27. Rotaciones de lenguajes regulares: Para un lenguaje L sea
el lenguaje consistente de transposiciones de dos partes en L.
Escriba un programa que dada una expresión regular E construya el autómata finito
 tal que
tal que
 ,
donde L(E) es el lenguaje expresado por E.
,
donde L(E) es el lenguaje expresado por E.
28. Autómatas no-deterministas- :
Un autómata no-determinista-
:
Un autómata no-determinista- (AND-
(AND- ) es un autómata no-determinista con la noción de reconocimiento cambiada: Una palabra es reconocida si toda computación, a partir de ella, en el autómata la conduce a un estado final. Escriba un programa que transforme a un AND-
) es un autómata no-determinista con la noción de reconocimiento cambiada: Una palabra es reconocida si toda computación, a partir de ella, en el autómata la conduce a un estado final. Escriba un programa que transforme a un AND- en un autómata finito equivalente.
en un autómata finito equivalente.




Siguiente: Autómatas de pila
Un nivel arriba: Expresiones regulares
Anterior: Ejercicios
Guillermo Morales-Luna
2000-06-27
 son indistiguibles si los estados a los que llegan, partiendo del inicial,
son indistiguibles si los estados a los que llegan, partiendo del inicial,
 tal que
tal que
 tal que
tal que
 de un único símbolo, que reconozca al lenguaje
de un único símbolo, que reconozca al lenguaje
 ,
donde L(E) es el lenguaje expresado por E.
Sugerencia: Razonando por inducción en la construcción de la expresión E, tranfórmela en una expresión que exprese al lenguaje
,
donde L(E) es el lenguaje expresado por E.
Sugerencia: Razonando por inducción en la construcción de la expresión E, tranfórmela en una expresión que exprese al lenguaje
![$L(\sqrt[n]{\mbox{\rm AF}})=\sqrt[n]{L(E)}$](img1693.gif) ,
donde L(E) es el lenguaje expresado por E.
Sugerencia: Razonando por inducción en la construcción de la expresión E, transfórmela en una expresión que exprese al lenguaje
,
donde L(E) es el lenguaje expresado por E.
Sugerencia: Razonando por inducción en la construcción de la expresión E, transfórmela en una expresión que exprese al lenguaje