



Next: F glider component (velocity
Up: T7
Previous: cross references
Contents
Figure:
T7's will not stack diagonally, but will almost do so when a little bit of buffer is included. Here the lattice is ``right seven in five generations,'' wherein two diagonal stripes are discernible.
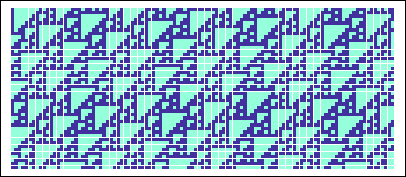 |
Figure:
One of the smallest lattices in which T7's participate is the shift-periodic lattice ``five left in eight generations.'' In this lattice there are two buffers between T7 stripes, one thick and one thin, which can alternate aperiodically.
 |
Figure:
More nearly horizontal stripes of T7's can be formed; the upper stripes rise to the right, whilst the lower stripes fall to the right. In both cases they are separated by a slight buffer.
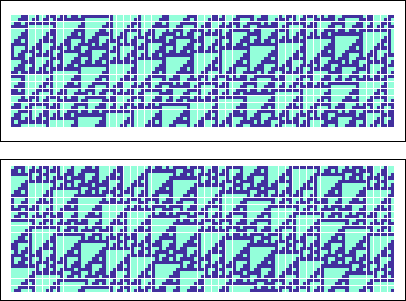 |
Figure:
There is no reason why composites cannot form, wherein two or more large triangles occupy the same unit cell. Here T6 and T7 combine to form diagonal stripes.
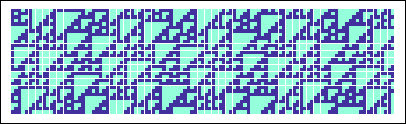 |
Figure:
Here T6, T7 and T9 combine to form diagonal stripes with a shift period of ``right 9 in 5.''
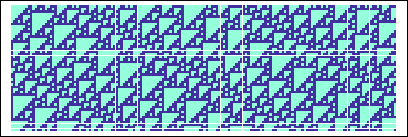 |




Next: F glider component (velocity
Up: T7
Previous: cross references
Contents
Jose Manuel Gomez Soto
2002-05-15





