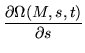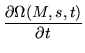


Next: sum of coefficients
Up: the matrizant
Previous: Picard's method
Another scheme of solution is to discretize the differential equation, approximating
dZ/dt = MZ by
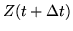 |
= |
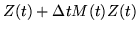 |
(246) |
| |
= |
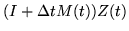 |
(247) |
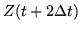 |
= |
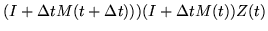 |
(248) |
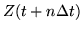 |
= |
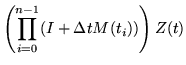 |
(249) |
| |
= |
![$\displaystyle \left[ I + \Delta t\sum_{i=0}^{n-1}M(t_i) +
\Delta t^2\sum_{i=0}^{n-1}\sum_{j<i} M(t_i)M(t_j) + \cdots\right] Z(t)$](img418.gif) |
(250) |
| |
= |
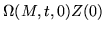 |
(251) |
These sums can be recognized as approximations to the integrals in Picard's method. However, this approximation is most useful in the product form, where the matrizant is sometimes called a product integral. For example, by observing the limits in the product, it is easy to conclude the rules
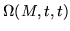 |
= |
I |
(252) |
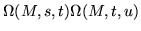 |
= |
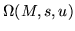 |
(253) |
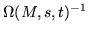 |
= |
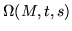 |
(254) |
Two further rules, which follow from the definitions, are



Next: sum of coefficients
Up: the matrizant
Previous: Picard's method
Microcomputadoras
2001-04-05
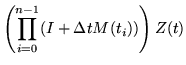
![$\displaystyle \left[ I + \Delta t\sum_{i=0}^{n-1}M(t_i) +
\Delta t^2\sum_{i=0}^{n-1}\sum_{j<i} M(t_i)M(t_j) + \cdots\right] Z(t)$](img418.gif)
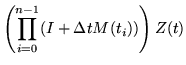
![$\displaystyle \left[ I + \Delta t\sum_{i=0}^{n-1}M(t_i) +
\Delta t^2\sum_{i=0}^{n-1}\sum_{j<i} M(t_i)M(t_j) + \cdots\right] Z(t)$](img418.gif)