Just as we had met heterocyclic flexagons before they were discussed
as such, so among the heterocyclic flexagons will find flexagons with
compound faces.
A compound face is one in which the two pats are of different face degrees.
Now, the face degree of a pat is the sum of the signs for the leaves in that
pat, except that alternate pats will have the sign of the face degree
reversed. The reason for this latter fact is that the sum of the entire sign
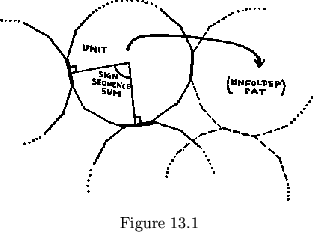
sequence is the angle between the perpendiculars on the hinges entering and
leaving the folded-together unit (see fig. 13.1). When one pat is unfolded
from the unit, as shown, it is turned upside down, so that its face degree
becomes negative in respect to that of the other pat. If
the face degrees of the two pats ![]() and
and ![]() are equal, we obtain the
followings: 13.1
are equal, we obtain the
followings: 13.1
![]()
![]()
Here, then, is merely a restatement of the rule that the sum of the
sign sequence must be congruent to zero,
![]() ; either this, or
its faces will be compound. Thus the magnitude of
; either this, or
its faces will be compound. Thus the magnitude of ![]() is a measure of how
compound a given face is;
is a measure of how
compound a given face is; ![]() is the difference in face degree between the
two pats making up any given face of the flexagon.
is the difference in face degree between the
two pats making up any given face of the flexagon.
In our discussion of heterocyclic flexagons, it was said in effect
that compound faces would be allowed only so long as
![]() . The reason for this was said to be
that when
. The reason for this was said to be
that when
![]() , binding results during
the flexing operation. This is still true. Most compound flexagons
(those whose faces are compound) can be operated only with difficulty, if
at all. In fact, they must be made of rather pliable material, as with
polycyclic flexagons of cycle greater than 4, since rigid leaves would
make flexing totally impossible. The reason for this annoying complication
is rather easier to observe than to explain. If the hinges entering and
leaving the folded-together unit do not coincide, a certain amount of
twist (varying with
, binding results during
the flexing operation. This is still true. Most compound flexagons
(those whose faces are compound) can be operated only with difficulty, if
at all. In fact, they must be made of rather pliable material, as with
polycyclic flexagons of cycle greater than 4, since rigid leaves would
make flexing totally impossible. The reason for this annoying complication
is rather easier to observe than to explain. If the hinges entering and
leaving the folded-together unit do not coincide, a certain amount of
twist (varying with ![]() ) will be imparted to the flexagon when each unit
is folded completely together. When we attempt to fold all the units
together simultaneously, this twist builds up and unwinds part of the
flexagon before we are finished. If, then, we try to flex one unit at a time,
we encounter trouble with the twist given the flexagon by flexing, itself.
However, this twist problem is of less magnitude than the preceding one,
so that it is practical, in most cases, to strain the flexagon to this
extent and flex each unit separately. Either this, or we can eliminate
the twist problem entirely by not folding the unit completely together
during flexing. In this way, the flexagon will flex all at once, but
the pats will be found to interfere with one another, thus binding the
flexing operation. In most cases the best procedure is to keep in mind
what one is attempting to do, and then simply feel around for the easiest
method of attaining the desired structure.
) will be imparted to the flexagon when each unit
is folded completely together. When we attempt to fold all the units
together simultaneously, this twist builds up and unwinds part of the
flexagon before we are finished. If, then, we try to flex one unit at a time,
we encounter trouble with the twist given the flexagon by flexing, itself.
However, this twist problem is of less magnitude than the preceding one,
so that it is practical, in most cases, to strain the flexagon to this
extent and flex each unit separately. Either this, or we can eliminate
the twist problem entirely by not folding the unit completely together
during flexing. In this way, the flexagon will flex all at once, but
the pats will be found to interfere with one another, thus binding the
flexing operation. In most cases the best procedure is to keep in mind
what one is attempting to do, and then simply feel around for the easiest
method of attaining the desired structure.
Why do we trouble ourselves with compound flexagons at all, if they
do not flex in a simple, respectable manner? It is because there are so
many compound flexagons. There are far more compound flexagons than
noncompound,
of course, but there are also far more compound flexagons than
there are heterocyclic flexagons. To find the compound flexagons made up
of one type of cycle only, we return to our proof that
![]() in
flexagons other than heterocyclic flexagons. This proof depends upon the
sign sequence substitution of groups of signs having equivalent sums, mod
in
flexagons other than heterocyclic flexagons. This proof depends upon the
sign sequence substitution of groups of signs having equivalent sums, mod
![]() .
The fact is that the substitution process, basic as it is, depends
only upon the changes that occur in the number sequence. These alter the
flexagon's structure; sign sequence changes alter only the positions of the
hinges and the shapes of the leaves. These latter have been shown to have
little relevance to the former; the two can actually proceed independently.
.
The fact is that the substitution process, basic as it is, depends
only upon the changes that occur in the number sequence. These alter the
flexagon's structure; sign sequence changes alter only the positions of the
hinges and the shapes of the leaves. These latter have been shown to have
little relevance to the former; the two can actually proceed independently.
Therefore, why can we not use arbitrary signs in the sign sequence
corresponding to a given number sequence, so long as hinges are not allowed
to intersect? The reasons that we have created rules to prevent doing this
are twofold: first, zero-faces might result. This would happen whenever
the leaf polygons would be made to coincide and complete cycles
would be used. Second, ![]() might not be congruent to zero. Both of these
complications have finally been accepted as members of the flexagon
family, so that the objections are overruled. With only one necessary
sign sequence restriction remaining, the shape of the flexagon can take on
unlimited variety.
might not be congruent to zero. Both of these
complications have finally been accepted as members of the flexagon
family, so that the objections are overruled. With only one necessary
sign sequence restriction remaining, the shape of the flexagon can take on
unlimited variety.
The main difference between compound and non-compound flexagons, as far
as general appearance is concerned, is that compound flexagons do not
lie about the center of the flexagon in an even ring of pats. Alternate
pats lie closer to the center than the others. The reason for this will be
seen by the reader as we progress. Compound flexagons usually require more
units than other flexagons. To determine how many units will be used in
a specific case, we must find the angle between the hinges entering and
leaving each unit. If the face degrees of the two pats are ![]() and
and ![]() , then
this angle,
, then
this angle, ![]() , is less than or equal to
, is less than or equal to
![]() . It may be less than
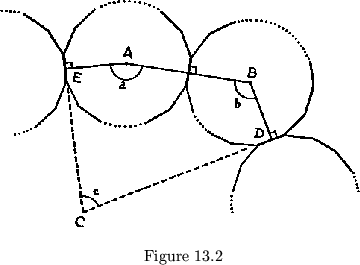
this value if the pats are folded partly together (see fig. 13.2). We may
note that if the polygon
. It may be less than
this value if the pats are folded partly together (see fig. 13.2). We may
note that if the polygon ![]() in the fig. 13.2 is concave at
in the fig. 13.2 is concave at ![]() or
or ![]() , a
correction of
, a
correction of
![]() for each concave angle must be added to the
expression above.
for each concave angle must be added to the
expression above.
The number of units used must then be at least
![]() and at least
2. Since this number does not contain the constant
and at least
2. Since this number does not contain the constant
![]() , the
number of units depends upon the face chosen for the determination. We
therefore choose the smallest face degree possible in the flexagon as
, the
number of units depends upon the face chosen for the determination. We
therefore choose the smallest face degree possible in the flexagon as ![]() .
Notice that
.
Notice that ![]() is congruent to the sum of the signs of the leaves in that
pat, while
is congruent to the sum of the signs of the leaves in that
pat, while ![]() is congruent to minus the sum of the signs of the leaves in
its pat.
is congruent to minus the sum of the signs of the leaves in
its pat.
In order to give an indication of the variety of compound flexagons, we will
arbitrarily limit ourselves in this discussion to flexagons made up of
coinciding regular leaves. These flexagons are perhaps the most picturesque
of the compound flexagons. To begin, we examine the possible faces for ![]() .
Other than
.
Other than
![]() , we have here only one possibility:
, we have here only one possibility:
![]() . Then the face degrees will be either
. Then the face degrees will be either
![]() or
or
![]() . (Faces one
of which is the negative of the other, such as
. (Faces one
of which is the negative of the other, such as
![]() and
and
![]() , are
not counted separately here. For this reason, we limit ourselves to just
one of the two possible values thus presented for
, are
not counted separately here. For this reason, we limit ourselves to just
one of the two possible values thus presented for ![]() ;
;
![]() is not considered.)
For the
is not considered.)
For the
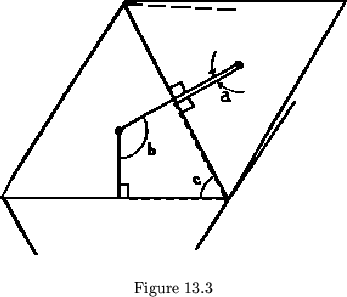
![]() face, we need
face, we need
![]() units (see fig. 13.3).
units (see fig. 13.3).
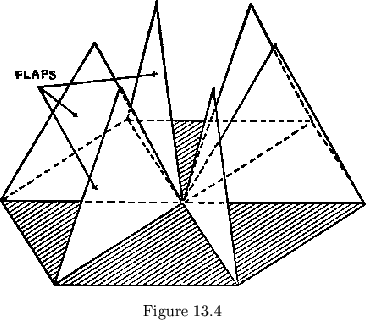
These lie in a hexagon, with flaps between the units (see fig. 13.4).
Clearly, whenever one pat has face degree ![]() , the flexagon will
require twice as many units as the corresponding non-compound flexagon with
face degree
, the flexagon will
require twice as many units as the corresponding non-compound flexagon with
face degree
![]() , yet look the same.
The
, yet look the same.
The
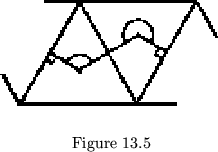
![]() face (fig. 13.5) apparently needs an infinite
number of units, since its hinges are parallel.
face (fig. 13.5) apparently needs an infinite
number of units, since its hinges are parallel.
When this is the case, we merely give the flexagon two units and do not permit it to lie flat. This face then would look like an octahedron with two opposite faces removed.
When ![]() , we have the possibilities
, we have the possibilities
![]() ,
,
![]() and
thereby the faces
and
thereby the faces
![]() ,
,
![]() ,
,
![]() and
and
![]() . From parallel
cases already considered we can eliminate
. From parallel
cases already considered we can eliminate
![]() ,
,
![]() and
and
![]() .
As for
.
As for
![]() , we need
, we need
![]() units, which will be arranged
in the hollow square shown in fig. 13.6.
units, which will be arranged
in the hollow square shown in fig. 13.6.
The flexagon
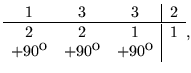
![]() , has three faces of this interesting type, and is the simplest
interesting compound flexagon, in its construction. For
, has three faces of this interesting type, and is the simplest
interesting compound flexagon, in its construction. For ![]() , all cases
but
, all cases
but
![]() and
and
![]() cannot lie flat:
cannot lie flat:
![]() units. But the
face
units. But the
face
![]() will lie flat, with five units, in the
handsome star shape of fig. 13.7.
As before, we can make a flexagon of this type with all ``+'' signs,
and therefore with all like faces, having
will lie flat, with five units, in the
handsome star shape of fig. 13.7.
As before, we can make a flexagon of this type with all ``+'' signs,
and therefore with all like faces, having ![]() . In fact, for
. In fact, for ![]() equal to
any integer
equal to
any integer ![]() the flexagon with the sign sequence
the flexagon with the sign sequence
![]() ,
,
![]() ,
,
![]() will have three like faces the degree of which will be
will have three like faces the degree of which will be
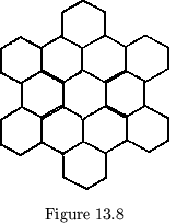
![]() ,
and all of which will lie flat. If
,
and all of which will lie flat. If ![]() , the flexagon
is shown in fig. 13.8. The other noteworthy faces for
, the flexagon
is shown in fig. 13.8. The other noteworthy faces for ![]() are
are
![]() ,
,
![]() and
and
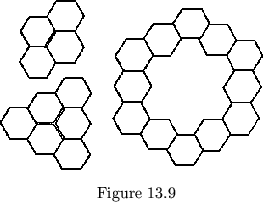
![]() .
These have the forms shown in fig. 13.9.
.
These have the forms shown in fig. 13.9.


The face degree
![]() is that of all the faces
of the flexagon with the sign sequence
is that of all the faces
of the flexagon with the sign sequence
![]() , except the cuts across
the diagonals of the square map. These faces are of degree
, except the cuts across
the diagonals of the square map. These faces are of degree
![]() , so
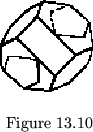
that they look like octahedrons with 2 opposite faces removed and the
corners clipped (fig. 13.10). The compound flexagons already given indicate
what will be found when we increase
, so
that they look like octahedrons with 2 opposite faces removed and the
corners clipped (fig. 13.10). The compound flexagons already given indicate
what will be found when we increase ![]() further.
further.
One very important question that remains unanswered is how we can
tell the face degree of a compound flexagon without actually experimenting.
This problem is easily dispelled when we remember that ![]() is a constant,
so that a computation of each value of
is a constant,
so that a computation of each value of ![]() or of
or of ![]() would give each value
of the other. If we are given the sign sequence and its map, we can compute
would give each value
of the other. If we are given the sign sequence and its map, we can compute
![]() immediately. To distinguish between the two different face degree
values, we can place them on opposite sides of path in the map. To
determine the face degrees, we begin by placing the sign sequence terms on
the outside of the map, next to their corresponding faces. The remainder
of the face degree numbers are computed by the rule that the face degree
term on the outside of a path is equal to the sum
immediately. To distinguish between the two different face degree
values, we can place them on opposite sides of path in the map. To
determine the face degrees, we begin by placing the sign sequence terms on
the outside of the map, next to their corresponding faces. The remainder
of the face degree numbers are computed by the rule that the face degree
term on the outside of a path is equal to the sum
![]() of the sign sequence terms lying on that side of the path, taken in the
direction indicated
by the path vectors. Hence, the term across a path from a given sign sequence
term will be
of the sign sequence terms lying on that side of the path, taken in the
direction indicated
by the path vectors. Hence, the term across a path from a given sign sequence
term will be
![]() where
where ![]() is the term. This
rule is merely an adaptation of the old method of computing face degrees,
pointing out that the two possible ways to calculate each face correspond
to the two possible values for each unit. It follows inmediately from
the fact that those leaves making up faces lying on one side of a given
face line in the map make up one pat of this face; those lying on the
other side make up the other pat. In computing face degrees, careful track
must be kept of the directions of the face vectors. Around the outside
edge of the map, these are understood to travel in one direction
about the map. Why have we said that the term across a path from a sign
is
is the term. This
rule is merely an adaptation of the old method of computing face degrees,
pointing out that the two possible ways to calculate each face correspond
to the two possible values for each unit. It follows inmediately from
the fact that those leaves making up faces lying on one side of a given
face line in the map make up one pat of this face; those lying on the
other side make up the other pat. In computing face degrees, careful track
must be kept of the directions of the face vectors. Around the outside
edge of the map, these are understood to travel in one direction
about the map. Why have we said that the term across a path from a sign
is
![]() , when it is to be equal to the sum of the signs
other than
, when it is to be equal to the sum of the signs
other than ![]() ? It is because of the direction of the face vectors.
Another way of viewing this is that the difference of the two face degrees
of each face must be
? It is because of the direction of the face vectors.
Another way of viewing this is that the difference of the two face degrees
of each face must be ![]() :
:
![]() .
.
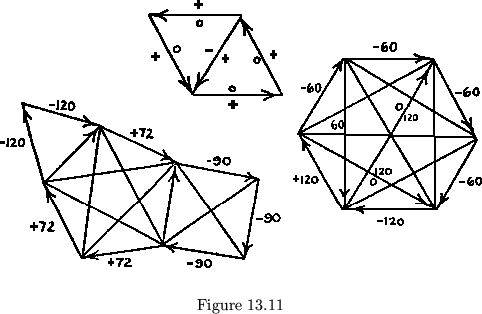
Three examples are shown in fig. 13.11: one for a flexagon with
re-gular coinciding leaves worked in degrees, one for a flexagon with
regular coinciding leaves worked on in terms of a definite ![]() , and
one for a heterocyclic flexagon made from regular leaves.
, and
one for a heterocyclic flexagon made from regular leaves.
This method at last gives us a strong tool for working effectively
with heterocyclics in which
![]() . We can now accurately predict
such
otherwise confusing data as which faces will be nearly or exactly zero
faces and which faces will not lie flat. We can also compute how many
units will be required to make any given face lie flat.
. We can now accurately predict
such
otherwise confusing data as which faces will be nearly or exactly zero
faces and which faces will not lie flat. We can also compute how many
units will be required to make any given face lie flat.