Other attempts can be made to find a sequence of faces which will show up in a linear or quasilinear order. A simple enough example would be take a line as a Tuckerman Tree,
with middle and Tukey Square diagrams
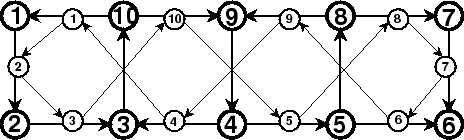
with polygon list
| + | + | + | - | + | - | - | - | + | - | + |
| 1 | 3 | 3 | 1 | 5 | 9 | 7 | 7 | 9 | 5 | 1 |
| 2 | 2 | 4 | 10 | 6 | 8 | 8 | 6 | 10 | 4 | 2 |
and frieze
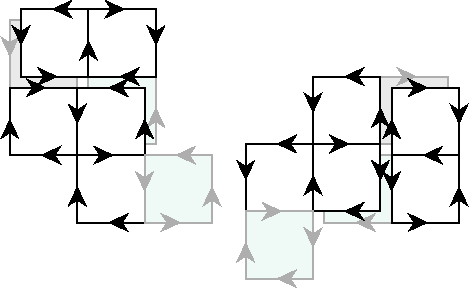
With a longer line as a Tuckerman Tree, the terminal ![]() 's will remain but there will be more
's will remain but there will be more ![]() alternations and depending on parity,
alternations and depending on parity, ![]() can become
can become ![]() . The
. The ![]() sequence tends to make the frieze curl up into a spiral, so the drawing ends up in two parts.
sequence tends to make the frieze curl up into a spiral, so the drawing ends up in two parts.
There is an interesting duality in flexagon construction, that spiral Tuckerman Trees tend to produce linear friezes, whereas linear trees tend to produce spiral friezes. It is not hard to figure out why, but it is curious nevertheless.