Segundo Caso.

Si $\phi$ imaginario, por ejemplo $\phi =i\beta \rightarrow \mu =e^{i\beta} =\cos\beta +i\,{\mbox{sen}}\beta$ por lo tanto el comportamiento de la cadena, corresponderá a un coseno o seno, con lo cual el movimiento de la cadena será del tipo ondulatorio, además si sacamos el módulo de $\mu$, esto es:

$$\vert e^{i\beta}\vert = \vert\mu\vert = (\cos^2\beta +\,{\mbox{sen}}^2\beta) = 1$$

Por lo tanto en este caso multiplicamos por un factor con valor absoluto ``1'', pero existirá un cambio de fase, aún cuando la amplitud se conserve constante, y es cuando generalmente se dice que existe movimiento ondulatorio. 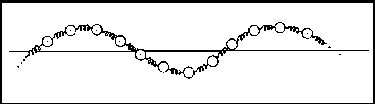Por otra parte para problemas físicos del tipo que estamos analizando, las raíces de los polinomios característicos que se obtienen, se suceden en parejas recíprocas (como se demostrará más adelante), por lo tanto si una raíz es compleja entonces existirá su conjugada, por lo cual es necesario considerar que: $\phi =\pm i\beta$ con lo que se obtiene $\mu =2\sqrt{1-\,{\mbox{sen}}^2\beta}$, por lo tanto el comportamiento de la cadena es ondulatorio, la gráfica que podemos considerar acorde con los datos anteriores será: