![\begin{displaymath}
\left[\begin{array}{cccccc}
a_0 & a_1 & a_2 & \cdots & a_...
...& a_1 \\
0 & & & & a_1 & a_0^{\prime}
\end{array}\right] =
\end{displaymath}](img901.gif)
![\begin{displaymath}
\left[\begin{array}{cccccc}
a_0 & a_1 & a_2 & \cdots & a_...
...& a_1 \\
0 & & & & a_1 & a_0^{\prime}
\end{array}\right] =
\end{displaymath}](img901.gif)
![\begin{displaymath}
\left[\begin{array}{ccccc}
-(a_1 +a_2) & 0 & \cdots & a_2...
... & 0 \\
a_1 & a_2 & & 0 & -a_1 -a_2
\end{array}\right] =D
\end{displaymath}](img902.gif) |
(10.1) |
Para obtener esta matriz, hemos usado algunas consideraciones ya
mencionadas con anterioridad, como son: el hecho de que estamos
tratando con un caso de interacciones a segundo vecinos, lo cual da
lugar a que en la matriz del modelo libre aparezcan los parámetros
nuevos ![]() y
y
![]() deducidos con anterioridad; otra cosa
que se puede apreciar es que las matrices para el caso libre y
cíclico, conservan la propiedad de que la suma de los elementos
de cada renglón es cero y es claro que la diferencia entre ellos
también conserva esta propiedad.
deducidos con anterioridad; otra cosa
que se puede apreciar es que las matrices para el caso libre y
cíclico, conservan la propiedad de que la suma de los elementos
de cada renglón es cero y es claro que la diferencia entre ellos
también conserva esta propiedad.
Además también podemos apreciar de la forma de la matriz
![]() , que el vector que tiene todos sus elementos iguales a uno, es un
eigenvector ya que si multiplicamos la matriz
, que el vector que tiene todos sus elementos iguales a uno, es un
eigenvector ya que si multiplicamos la matriz ![]() por este vector, el
resultado es que se va a sumar cada renglón y cada renglón sumado
resulta cero, esto es:
por este vector, el
resultado es que se va a sumar cada renglón y cada renglón sumado
resulta cero, esto es:
![\begin{displaymath}
\left[\begin{array}{ccccc}
-a_1 -a_2 & 0 & \cdots & a_2 &...
...in{array}{c}
0 \\ 0 \\ \vdots \\ 0 \\ 0 \\ \end{array}\right]
\end{displaymath}](img905.gif)
Por lo tanto estamos tratando con el eigenvector correspondiente al eigenvalor cero, lo cual quiere decir que los desplazamientos son los mismos para cada elemento de la cadena, por lo tanto a un anillo y una cadena libre les es permitido un movimiento de traslación de todos los elementos que los constituyen.
En el caso de la cadena, que está fija en sus extremos, no es
aplicable lo anterior y por lo tanto el vector con componentes 1's, no
es eigenvector, ya que en este caso no existen los elementos de las
esquinas que se forman por efectos del caso libre (esto es el
![]() y
y
![]() ).
).
Ahora lo que nos interesa es analizar las propiedades de la
matriz ![]() , es posible obtener sus eigenvalores y eigenvectores en una
forma inmediata, debido a que la parte del centro contiene puros ceros
y por lo tanto únicamente una parte, que forma una matriz de
, es posible obtener sus eigenvalores y eigenvectores en una
forma inmediata, debido a que la parte del centro contiene puros ceros
y por lo tanto únicamente una parte, que forma una matriz de
![]() , es la que realmente nos interesa.
, es la que realmente nos interesa.
Para analizar la matriz ![]() es conveniente factorizar en la
forma siguiente.
es conveniente factorizar en la
forma siguiente.
![\begin{displaymath}
D=-a_2 II+\left[\begin{array}{rccr}
-a_1 & 0 & a_2 & a_1 ...
...& 0 \\
a_1 & a_2 & 0 & -a_1 \end{array}\right] =D_1 -a_2 II
\end{displaymath}](img906.gif)
Los eigenvalores de la matriz ![]() se obtienen de
se obtienen de
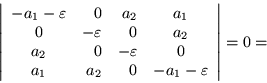
Por lo tanto las raíces para estas ecuaciones son
respectivamente
| (10.2) |
Estos son los eigenvalores de la matriz ![]() , pero los que
necesitamos son los de la matriz
, pero los que
necesitamos son los de la matriz ![]() que son
que son
Esto es debido a que el parámetro ![]() únicamente afecta a
la diagonal de la matriz
únicamente afecta a
la diagonal de la matriz ![]() y por consiguiente a sus eigenvalores;
como se puede ver estos eigenvalores son todos ``negativos''; para los
eigenvalores
y por consiguiente a sus eigenvalores;
como se puede ver estos eigenvalores son todos ``negativos''; para los
eigenvalores
![]() y
y
![]() esta afirmación es clara, para los
otros dos es necesario aplicar la desigualdad de Schwarz para
comprobarlo, esto es:
esta afirmación es clara, para los
otros dos es necesario aplicar la desigualdad de Schwarz para
comprobarlo, esto es:
Sabemos que
| (10.3) |
Con este resultado podemos concluir que los dos últimos
eigenvalores son negativos. Entonces como todos los eigenvalores son
negativos o cero, resulta que la matriz ![]() es negativa semidefinida,
es decir cumple la desigualdad.
es negativa semidefinida,
es decir cumple la desigualdad.
| (10.4) |
Por lo tanto la matriz ![]() , que representa el problema
cíclico menos el de extremos libres, proporciona una relación de
orden sujeta a todas las propiedades aritméticas.
, que representa el problema
cíclico menos el de extremos libres, proporciona una relación de
orden sujeta a todas las propiedades aritméticas.
O sea que la matriz ![]() , es la atriz que tiene que ser sumada a
la matriz no-cíclica para obtener la cílcica, por esto, es
conveniente encontrar una relación de orden entre los eigenvalores
de la matriz cíclica (que denotamos
, es la atriz que tiene que ser sumada a
la matriz no-cíclica para obtener la cílcica, por esto, es
conveniente encontrar una relación de orden entre los eigenvalores
de la matriz cíclica (que denotamos ![]() ), con la matriz de
extremos libres (que denotamos por
), con la matriz de
extremos libres (que denotamos por ![]() ).
).
Partiendo de una relación anterior
| (10.5) |
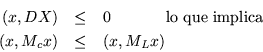
Este último resultado implica, que si ordenamos los
eigenvalores algebraicamente y en parejas, en cada una de estas
matrices, los eigenvalores de ![]() siempre van a ser mayores que los
de
siempre van a ser mayores que los
de ![]() . Este resultado se puede visualizar mejor en forma gráfica
. Este resultado se puede visualizar mejor en forma gráfica
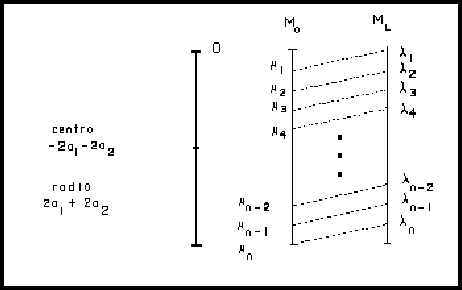
Por lo tanto una onda de frecuencia alta es posible en el
sistema cíclico. Para analizar los resultados anteriores es
necesario usar el hecho de que
Ya que siempre ![]() entonces la raíz cuadrada es
imaginaria pura, lo cual es correcto, ya que las frecuencias que no
son otra cosa que los exponentes, son imaginarios puros que conducen a
una exponencial real de una onda, entonces, a mayor
entonces la raíz cuadrada es
imaginaria pura, lo cual es correcto, ya que las frecuencias que no
son otra cosa que los exponentes, son imaginarios puros que conducen a
una exponencial real de una onda, entonces, a mayor ![]() (en
valor absoluto) la frecuencia es mayor, pero también implica que el
módulo es más negativo, esto quiere decir, que el sistema
cíclico tiene frecuencias que son mayores, cada una de ellas, a
las correspondientes al sistema con extremos libres; esto se puede
apreciar cuando hacemos vibrar, a una barra y un anillo que tengan la
misma longitud, el resultado es una desigualdad; esto para los
primeros eigenvalores no pasa, ya que hemos visto que son cero y en
los demás existe la posibilidad de que sean iguales.
(en
valor absoluto) la frecuencia es mayor, pero también implica que el
módulo es más negativo, esto quiere decir, que el sistema
cíclico tiene frecuencias que son mayores, cada una de ellas, a
las correspondientes al sistema con extremos libres; esto se puede
apreciar cuando hacemos vibrar, a una barra y un anillo que tengan la
misma longitud, el resultado es una desigualdad; esto para los
primeros eigenvalores no pasa, ya que hemos visto que son cero y en
los demás existe la posibilidad de que sean iguales.