Debido a la gran importancia que tienen los paréntesis de Poisson en la mecánica clásica, así como su generalización en la mecánica cuántica que son los conmutadores, es conveniente axiomatizar el concepto de paréntesis de Poisson.
Axioma 1. Antisimetría
Axioma 2. Linealidad
Axioma 3. Identidad de Jacobi
Axioma 4. ``Derivada"
Este es un momento apropiado para hablar acerca de nuestro sistema de axiomas.
En primer lugar mostramos una consecuencia inmediata de 1.
Inmediatamente se puede probar, usando 1, y 2 que
El axioma tres es la propiedad que reemplazará a la asociatividad.
El hecho de que al axioma 4 le hallamos puesto el título de derivada se debe a que:
Una derivada D es un operador tal que
D1)
![]()
D2)
![]()
D3)
![]()
D4)
![]()
Los axiomas 1, 2, 3 nos dicen que los paréntesis de Poisson forman un
álgebra de Lie.
El axioma 2 por si solo nos asegura que tenemos un operador lineal y los axiomas 2, 4 que tenemos casi definida una derivada.
Es conveniente hacer notar que el paréntesis de Poisson es un operador lineal, cuando dejamos fijo uno de los argumentos y esto mismo sucede cuando hablamos de que si es casi una derivada.
Al respecto hemos escrito anteriormente casi una derivada ya que el inciso D4 de la definición de derivada no se cumple, y esto es lo que nos va a traer como concecuencia es que no tendremos unicidad. Sin embargo de aquí en adelante diremos que los paréntesis de Poisson forman un álgebra de Lie con derivada.
Ahora es conveniente hacer notar que el paréntesis de Poisson definido
como
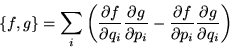
Hay que hacer notar aquí, que cualquier conjunto con una estructura tal que cumpla con esos axiomas se comportará como los paréntesis de Poisson definidos como una suma de productos de derivadas parciales.
Para ver que los paréntesis de Poisson cumplen con los axiomas escribamos
![]() ,
, ![]() de la siguiente manera.
de la siguiente manera.
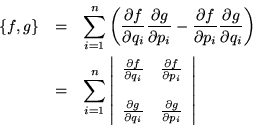
A1)
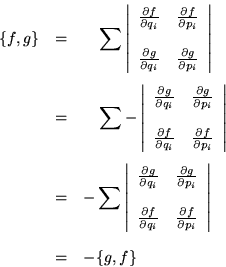
A2)
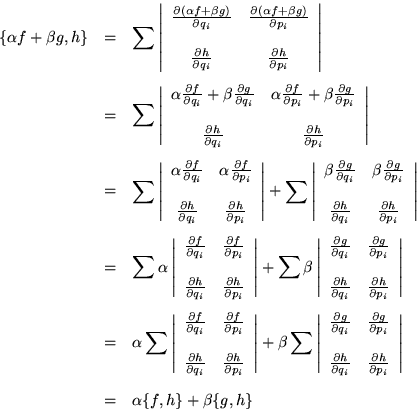
A4)
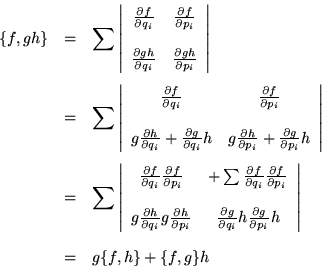
Otra cosa que es importante verificar es que ![]() con respecto
a las variables canónicas
con respecto
a las variables canónicas ![]() , y
, y ![]() , que denotaremos por
, que denotaremos por ![]() es igual a
es igual a ![]() con respecto a cualquier otra colección de variables
canónicas. Esto justifica hasta cierto punto el hecho de haber definido
los paréntesis de Poisson sin escribir las variables.
con respecto a cualquier otra colección de variables
canónicas. Esto justifica hasta cierto punto el hecho de haber definido
los paréntesis de Poisson sin escribir las variables.
Así se prueba que
En realidad podemos hacer esta afirmación si pasamos de las variables
![]() ,
, ![]() por medio de una transformación canónica a las variables
por medio de una transformación canónica a las variables ![]() ,
, ![]() .
.
Si nuestra transformación no es canónica no podemos asegurar nada.