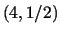 reversible cellular automaton, rule FFAA5500
reversible cellular automaton, rule FFAA5500
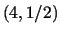 reversible cellular automaton, rule FFAA5500
reversible cellular automaton, rule FFAA5500
This automaton has Welch indices ![]() and
and ![]() . The evolution rule, an example of the evolution, and its block permutations are the following:
. The evolution rule, an example of the evolution, and its block permutations are the following:
The connectivity relation associated with this automaton is the following:
![\includegraphics[width=5in]{imagenes/example12}](img156.gif)
|
The transitive closure of connectivity relation associated with this automaton is the following:
![\includegraphics[width=5in]{imagenes/example13a}](img157.gif)
|
If we rearrange this transitive closure, we obtain the following classes:
In this case we see that the automaton have ![]() equivalence classes,
equivalence classes, ![]() of
of ![]() elements each one and
elements each one and ![]() of one element. Take the block
of one element. Take the block ![]() representing the sequence of states
representing the sequence of states ![]() . This block has period
. This block has period ![]() , so the configuration formed with repetitions of the sequence
, so the configuration formed with repetitions of the sequence ![]() must have period
must have period ![]() . We have to remember that we are using the composition of the original evolution rule for keeping the same position when we compare configurations. In this way, the period
. We have to remember that we are using the composition of the original evolution rule for keeping the same position when we compare configurations. In this way, the period ![]() is truly a period
is truly a period ![]() in the evolution of the automaton. An example of this periodical behavior is the following:
in the evolution of the automaton. An example of this periodical behavior is the following:
![\includegraphics[width=5in]{imagenes/example14}](img163.gif)
|
Now, we will see all the possible mappings among sequences of ![]() cells using the process described in section 5.4. For example, the mapping of
cells using the process described in section 5.4. For example, the mapping of ![]() is the following:
is the following:
Calculating all the possible mappings among sequences of ![]() cells, and taking such sequences as centered cylinder sets, we have the following mapping among centered cylinder sets:
cells, and taking such sequences as centered cylinder sets, we have the following mapping among centered cylinder sets:
![\includegraphics[width=5in]{imagenes/example16}](img165.gif)
|
The transitive closure of the mapping among centered cylinder sets is the following:
![\includegraphics[width=5in]{imagenes/example17}](img166.gif)
|
Since we only have one equivalence class and there exists centered cylinder sets that can be fixed, then this automaton has topologically mixing orbits. For example, we can form an orbit from the centered cylinder set
![]() to the centered cylinder set
to the centered cylinder set
![]() in
in ![]() steps, corresponding to
steps, corresponding to ![]() evolutions because the composition of the evolution rule. We use the recurrent centered cylinder set
evolutions because the composition of the evolution rule. We use the recurrent centered cylinder set
![]() for constructing such an orbit.
for constructing such an orbit.
But, since the centered cylinder set
![]() can be fixed, we can use it to get an orbit from the centered cylinder set
can be fixed, we can use it to get an orbit from the centered cylinder set
![]() to the centered cylinder set
to the centered cylinder set
![]() in
in ![]() steps.
steps.