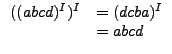


Next: Operaciones con lenguajes
Up: Alfabetos y lenguajes
Previous: Alfabetos, cadenas y lenguajes
Contents
Ahora describiremos algunas de las características de las cadenas y operaciones básicas que se pueden realizar con ellas.
Si 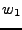 y
y 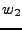 son cadenas, la concatenación de éstas dos cadenas resulta en la cadena que se obtiene al agregar la segunda al final de la primera, es decir, si tenemos
son cadenas, la concatenación de éstas dos cadenas resulta en la cadena que se obtiene al agregar la segunda al final de la primera, es decir, si tenemos 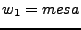 y
y 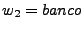 , la concatenación de estas dos cadenas es
, la concatenación de estas dos cadenas es 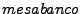 y se denota
y se denota
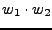 o
o 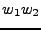 , por lo que podemos observar que
, por lo que podemos observar que
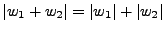 . La concatenación de cualquier cadena
. La concatenación de cualquier cadena 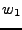 con la cadena vacía
con la cadena vacía
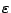 deja intacta a la cadena
deja intacta a la cadena 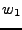 . La igualdad entre cadenas se denota con el signo `
. La igualdad entre cadenas se denota con el signo `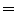 ' y se dá cuando dos o más cadenas tienen exactamente los mismos símbolos en la misma posición y tienen la misma longitud.
' y se dá cuando dos o más cadenas tienen exactamente los mismos símbolos en la misma posición y tienen la misma longitud.
Ejemplo: Si 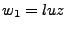 y
y 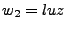 , entonces
, entonces 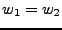 .
.
La potencia de una cadena sobre un alfabeto quiere decir que tomamos toda la cadena como una unidad atómica, es decir, si 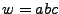 , entonces
, entonces
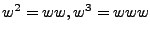 y así sucecivamente. Lo anterior lo podemos simplificar con la siguiente definición.
y así sucecivamente. Lo anterior lo podemos simplificar con la siguiente definición.
Por lo tanto si 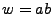 sobre el alfabeto
sobre el alfabeto
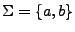 , tenemos que
, tenemos que
y podemos continuar hasta la i-ésima potencia de 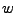 , que denotaremos como
, que denotaremos como 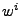 .
.
Ahora trataremos con el sufijo y el prefijo de una cadena, si tenemos una cadena 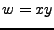 , donde
, donde 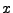 y
y 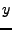 también son cadenas, entonces
también son cadenas, entonces 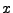 es el prefijo de
es el prefijo de 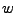 y
y 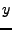 es el sufijo, hay que recordar que la cadena vacía puede ser el prefijo de cualquier cadena, además, si tenemos que
es el sufijo, hay que recordar que la cadena vacía puede ser el prefijo de cualquier cadena, además, si tenemos que 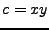 , donde
, donde 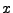 es el prefijo de
es el prefijo de 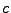 y
y
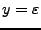 , entonces resulta que
, entonces resulta que 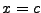 , lo cual indica que toda cadena es prefijo de si misma.
, lo cual indica que toda cadena es prefijo de si misma.
Una cadena 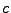 es una subcadena o subpalabra de otra cadena
es una subcadena o subpalabra de otra cadena 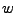 , si exiten cadenas
, si exiten cadenas 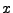 y
y 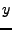 para las cuales
para las cuales 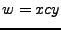 .
.
La inversa o transpuesta de una cadena 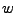 se denota como
se denota como 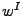 y quiere decir que, si se tiene
y quiere decir que, si se tiene 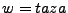 , entonces
, entonces 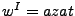 . Más generalmente podemos decir que
. Más generalmente podemos decir que
Para ver como funciona la definición anterior utilizaremos un ejemplo, si se tiene 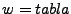 , al aplicar la definición, se logra lo siguiente:
, al aplicar la definición, se logra lo siguiente:
La inversa de una cadena tiene ciertas características, con la concatenación de cadenas, por ejemplo, si se tienen cadenas ab y cd que al concatenarse forman abcd, sabemos que
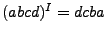 , de lo cual podemos observar que
, de lo cual podemos observar que
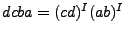 . Por lo tanto, si
. Por lo tanto, si  y
y 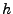 son cadenas y si
son cadenas y si 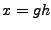 , entoces
, entoces
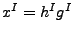 .
.
La inversa se anula a si misma, es decir, si a una cadena 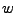 se le aplica la inversa dos veces seguidas, el resultado será
se le aplica la inversa dos veces seguidas, el resultado será 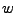 , como si no se hubiera aplicado ni una vez. Más generalmente,
, como si no se hubiera aplicado ni una vez. Más generalmente, 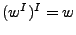 .
.
Ejemplo:



Next: Operaciones con lenguajes
Up: Alfabetos y lenguajes
Previous: Alfabetos, cadenas y lenguajes
Contents
Pablo Gerardo Padilla Beltrán
2005-10-21
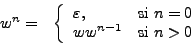
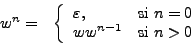
![]() sobre el alfabeto
sobre el alfabeto
![]() , tenemos que
, tenemos que
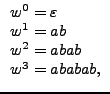
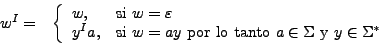
![]() , al aplicar la definición, se logra lo siguiente:
, al aplicar la definición, se logra lo siguiente:
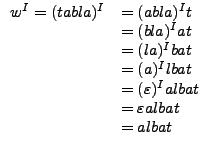
![]() , de lo cual podemos observar que
, de lo cual podemos observar que
![]() . Por lo tanto, si
. Por lo tanto, si ![]() y
y ![]() son cadenas y si
son cadenas y si ![]() , entoces
, entoces
![]() .
.
![]() se le aplica la inversa dos veces seguidas, el resultado será
se le aplica la inversa dos veces seguidas, el resultado será ![]() , como si no se hubiera aplicado ni una vez. Más generalmente,
, como si no se hubiera aplicado ni una vez. Más generalmente, ![]() .
.