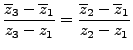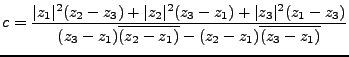Next: Ejemplo 2
Up: Aplicaciones geométricas
Previous: Aplicaciones geométricas
Contents
Encontrar la forma general de un círculo que pasa por 3 puntos dados
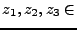 C
C
Solución.-
La definición de círculo esta definida como el lugar geométrico en el cual la distancia de todos sus puntos es igual a otro punto llamado centro. Entonces la ecuación de un círculo será
siendo 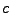 el número complejo que corresponde al centro. Si elevamos todo al cuadrado
Resolviendo la multiplicación tendremos
esta será la ecuación general de un círculo con centro
el número complejo que corresponde al centro. Si elevamos todo al cuadrado
Resolviendo la multiplicación tendremos
esta será la ecuación general de un círculo con centro 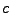 y radio
y radio 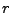 . Sustituyendo los anteriores puntos tendremos 3 ecuaciones
si restamos la primera ecuación a la segunda y luego a la tercera nos quedará
. Sustituyendo los anteriores puntos tendremos 3 ecuaciones
si restamos la primera ecuación a la segunda y luego a la tercera nos quedará
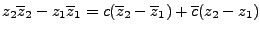 |
(5) |
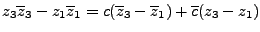 |
(6) |
Podemos acomodar estas dos ecuaciones de forma matrícial usando las relaciones de la ecuación ![[*]](file:/usr/share/latex2html/icons/crossref.png) en el primer renglón y la ecuación
en el primer renglón y la ecuación ![[*]](file:/usr/share/latex2html/icons/crossref.png) en el segundo renglón.
Si el determinante de la matriz 2x2 es igual a cero cumple que
lo cual es la condición necesaria para que los 3 puntos no sean colineales.
Si obtenemos la matriz inversa de la matriz de dos por dos y la multiplicamos por la matriz del lado izquierdo podremos tener el valor de
en el segundo renglón.
Si el determinante de la matriz 2x2 es igual a cero cumple que
lo cual es la condición necesaria para que los 3 puntos no sean colineales.
Si obtenemos la matriz inversa de la matriz de dos por dos y la multiplicamos por la matriz del lado izquierdo podremos tener el valor de 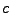 el cual estará dado por
el radio lo podemos obtener con
el cual estará dado por
el radio lo podemos obtener con
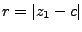 .
.
{(JS1pJS2pJS3p;)i
(R1Pj*R2R3-* R2Pj*R3R1-* R3Pj*R1R2-* ++ ;)a
( R1 j R2 R3 - * R2 j R3 R1 - * R3 j R1 R2 - * ++ ;)b
(@a@b/;)c
(R1 @c-Pj*r;)R
(
(@i @c @R k;)
(R1zpR2zpR3zp;)
;)}
Figura:
Resultado del programa que genera un círculo que pasa por puntos dados
|
|




Next: Ejemplo 2
Up: Aplicaciones geométricas
Previous: Aplicaciones geométricas
Contents
Julio N. Argota Q.
2006-09-28
![$\displaystyle \left[ \begin{array}{rl}
z_2\overline z_2-z_1\overline z_1 \\
z_...
...{array} \right]
\left[ \begin{array}{rl}
c \\
\overline c
\end{array} \right]
$](img167.png)