



Next: The matrices
Up: Diagrams
Previous: the pair diagram
A Welch diagram is a subdiagram of the subset diagram, characterized for surjective automata as consisting of the largest subsets accessible from the unit classes. The common order of all its subsets is the Welch index for that automaton, left or right according to the handedness of the subset diagram. For any given label, the links bearing that label form trees when all states are quiescent.
The Welch diagram is important because it is an image of the de Bruijn diagram within the subset diagram. By image is meant that the same paths are encountered irrespective of the diagram, so let us suppose that M and N are the connection matrices of the two diagrams, and that L is a mapping from one diagram to the other. The requirement is then
A good candidate for L is the membership matrix; the rows of L are indexed by nodes in the de Bruijn diagram, the columns in turn being indexed by subsets in the subset diagram. Consequently L is an
 matrix whose elements are the predicates
matrix whose elements are the predicates
| Li,S |
 |
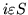 |
(47) |
The equivalence of M and N then depends upon
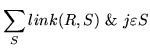 |
= |
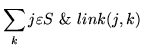 |
(48) |




Next: The matrices
Up: Diagrams
Previous: the pair diagram
root
2000-03-17