



Next: orthogonality
Up: Quaternions versus elementary matrices
Previous: multiplication table
Anyway, splitting the sum into scalar plus vector gives
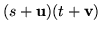 |
= |
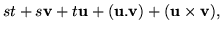 |
(49) |
particular interest attaching to the case where s and t are zero, leaving the product of two vectors to take the form of a scalar plus a vector. This inner (or dot) product is not the usual one, but one using a Minkowski metric:
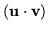 |
= |
- u1 v1 + u2 v2 + u3 v3, |
(50) |
| |
= |
![$\displaystyle \left[ \begin{array}{ccc}
u_1 & u_2 & u_3
\end{array} \right]
\le...
...rray} \right]
\left[ \begin{array}{c}
v_1 \\ v _2 \\ v_3
\end{array} \right].$](img178.gif) |
(51) |
Since the Minkowski inner product can be positive, negative, or zero, taking it for the square of a norm requires considering the sign, unless an imaginary norm is acceptable. So to define the norm of a vector, use the absolute value of the metric, by setting
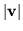 |
= |
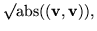 |
(52) |
which can vanish for a nonzero vector, and never forgetting the possible influence of the bypassed sign.
Since the special theory of relativity contains the best known uses of the Minkowslki metric, it is convenient to adopt the physical vocabulary according to which vectors whose squared norm is positive are spacelike, timelike for a negative square, and null when it is zero.
subsubsectionvector product
In turn the vector product differs slightly from its cartesian version, reading
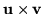 |
= |
 |
(53) |
| |
= |
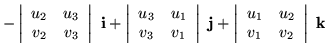 |
(54) |
| |
|
|
(55) |
| |
= |
 |
(56) |
This symbolic determinant works out well enough, differing from the classical formula only by the sign associated with 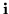 .
The notation makes it immediately apparent that
.
The notation makes it immediately apparent that
 and that
and that
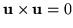 .
.
Interestingly enough,
 |
= |
 |
(57) |
the minus sign in he inner product cancelling the minus in the vector product. So the formula for Euclidean volume can still be used to check for the linear dependence of vectors. The formula can be used to confirm that in the Minkowski metric, the vector product is Minkowski-orthogonal to its factors, in complete analogy to the Euclidean formula. However, if we are interested in the whole plane which is Minkowski-orthogonal to a given vector, it will be inclined relative to what would be expected from Euclidean orthogonality.




Next: orthogonality
Up: Quaternions versus elementary matrices
Previous: multiplication table
root
2000-03-17
![$\displaystyle \left[ \begin{array}{ccc}
u_1 & u_2 & u_3
\end{array} \right]
\le...
...rray} \right]
\left[ \begin{array}{c}
v_1 \\ v _2 \\ v_3
\end{array} \right].$](img178.gif)
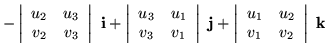

![]() .
The notation makes it immediately apparent that
.
The notation makes it immediately apparent that
![]() and that
and that
![]() .
.
