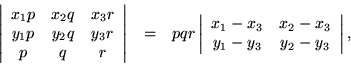
Applying the foregoing ideas to a plane, suppose that three points are represented projectively. Then their determinant is
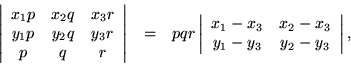
If there were a second triangle,
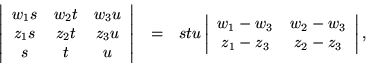
Just as in the two-dimensional version, it should be possible to find a permutation of the six points for which the multipliers cancel, leaving a combination of determinants as an invariant.
 |
One suggestion would be to exchange the points chosen as origins.
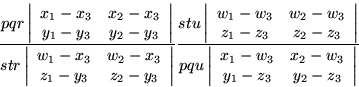 |
(2) |
A further suggestion would be to notice that of the six points, one stays fixed while the others get shuffled around. Therefore it could be made to coincide with one of the others, giving an invariant depending on five points rather than six, which could be of both symbolic and computational advantage.