Bibliography

1

Enrique Suárez Íñiguez, ``Por qué la tesis de licenciatura debe desaparacer,'' Ciencia 50 58-62 (Junio de 1999).

2

Martín Aluja Schuneman, Rogelio Macías Ordíñez y Pedro Bosch Giral, ``Por qué la tesis de licenciatura NO debe desaparacer,'' Ciencia 50 45-49 (Septiembre de 1999).

3

Shahen Hacyan, ``Y usted, ¿cuántas citas tiene?'' Ciencia 50 54-57 (Junio de 1999).

Cross Ratio

4

E. A. Maxwell, The Methods of Plane Projective Geometry based on the use of General Homogeneous Coordinates, Cambridge, at the University Press, 1963.

5

E. A. Maxwell, General Homogeneous Coordinates in Space of Three Dimensions, Cambridge, at the University Press, 1961.

6

Lancelot Hogben, El Universo de los números, Ediciones Destino, Barcelona, 1966, p. 145.

7

Dirk J. Struik, Lectures on Analytic and Projective Geometry, Addison-Wesley Publishing Company, Inc., Cambridge, Massachusetts, 1953.

8

Kenichi Kanatani, Group-Theoretical Methods in Image Understanding, Springer Verlag, Berlin, 1990 (ISBN 3-540-51253-5).

9

Richard O. Duda and Peter E. Hart, Pattern Classification and Scene Analysis, John Wiley and Sons, New York, 1973 (ISBN 0-471-22361-1).

10

Joseph L. Mundy and Andrew Zisserman (Eds.), Geometric Invariance in Computer Vision, The MIT Press, Cambridge, Massachussetts, 1992 (ISBN 0-262-13285-0).

11

Joseph L. Mundy, Andrew Zisserman and David Forsyth (Eds.), ``Application of Invariance in Computer Vision,'' Lecture Notes in Computer Science 825, Springer-Verlag, New York, 1994 (ISBN 0-387-58240-1).

12

Thomas H. Reiss, ``Recognizing Planar Objects Using Invariant Image Feartures,'' Lecture Notes in Computer Science 676, Springer-Verlag, New York, 1993 (ISBN 0-387-56713-5).

13

T. Gevers and A. W. M. Smeulders, ``Efficient recognition of 3-D rigid solid objects from 2-D projective images based on projective invariant descriptions,'' SPIE Volume 2357, pp. 296-302.

14

Hazem F. Barakat and Edward M. Mikhail, ``Object model construction by invariance and photogrammetry,'' SPIE Volume 3072, pp. 295-306.

15

Eamon B. Barrett, Paul M. Payton, Peter J. Marra, and Michael H. Brill, ``Geometric Interpretations of Algebraic Invariants in Images of 3D Scenes,'' SPIE Volume 3168 pp 286-299.

16

Adolf Hurwitz and Richard Courant, Vorlesungen über Allgemeine Funktionentheorie und Elliptische Funktionen, Verlag von Julius Springer, Berlin, 1925.

Putzer's Method

17

F. Silva Leite and P. Crouch, ``Closed forms for the exponential mapping on matrix Lie groups based on Putzer's method,'' Journal of Mathematical Physics 40 3561-3568 (1999).

18

E. J. Putzer, ``Avoiding the Jordan canonical form in the discussion of linear systems with constant coefficients,'' American Mathematical Monthly 73 2-7 (1966).

19

Cleve Moler and Charles van Loan, ``Nineteen dubious ways to compute the exponential of a matrix,'' SIAM Review 20 801-836 (1978).

20

R. B. Kirchner, ``An explicit formula for e^At,'' American Mathematical Monthly 74 1200-1204 (1967).

21

M. Kwapisz, ``The power of a matrix,'' SIAM Review 40 703-705 (1998).

22

Shui-Hung Hou, ``A simple proof of the Leverrier-Faddeev characteristic polynomial algorithm,'' SIAM Review 40 706-709 (1998).

23

I. E. Leonard, ``The matrix exponential,'' SIAM Review 38 507-512 (1996).

24

Eduardo Liz, ``A note on the matrix exponential,'' SIAM Review 40 700-702 (1998).

25

Jack Macki, ``Three Notes on the Exponential of a Matrix and Applications,'' SIAM Review 40 699-699 (1998).

26

I. Gohberg, P. Lancaster, and L. Rodman, Invariant Subspaces of Matrices with Applications, John Wiley and Sons, Inc., New York, 1986 (ISBN 0-471-84260-5).

27

A. I. Mal'cev, Foundations of Linear Algebra, W. H. Freeman and Company, San Francisco and London, 1963.

28

Saber N. Elaydi and William A. Harris, Jr., ``On the computation of A^N,'' SIAM Review 40 965-971 (1998).

29

Edward P. Fulmer ''Computation of the matrix exponential,'' American Mathematical Monthly 82 156-159 (1975).

30

Tom M. Apostol, ``Explicit formulas for solutions of the second-order matrix differential equation Y''=AY,'' American Mathematical Monthly 82 159-162 (1975).

31

F. R. Gantmacher, The Theory of Matrices, volume 1, volume 2, Chelsea Publishing Company, New York, 1959.

Reversible Automata

46

Jarkko Kari, ``Representation of Reversible Cellular Automata with Block Permutations,'' Mathematical Systems Theory 29 47-61 (1996).

43

G. A. Hedlund, ``Endomorphisms and automorphisms of the shift dynamical system,'' Mathematical Systems Theory 3 320-375 (1969).

34

Harold V. McIntosh, ``Cellular Automata via de Bruijn diagrams,'' 1990.

35

S. Amoroso and G. Cooper, ``The Garden of Eden theorem for finite configurations,'' Proceedings of the American Mathematical Society 26 158-164 (1970)

36

S. Amoroso and Y. N. Patt, ``Decision Procedures for Surjectivity and Injectivity of Parallel Maps for Tesselation Structures,'' Journal of Computer and System Sciences 6 448-464 (1972).

37

Mike Boyle, ``Symbolic Dynamics and Matrices,'' in ``Combinatorial and Graph-Theoretical Problems in Linear Algebra,'' IMA Volumes in Mathematics and its Applications, Vol. 50, Academic Press, New York, 1993, pp 1-38.

38

Fan R. K. Chung, ``Spectral Graph Theory,'' CBMS Regional Conference Series in Mathematics Number 92, American Mathematical Society, Providence, 1997.

39

Dragos M. Cvetkovic, Michael Doob, and Horst Sachs, Spectra of Graphs, Academic Press, New York, 1979.

74

P. Fatou, ``Sur les équations fonctionelles (premiere mémoire),'' Bulletin de la Societe Mathematique de France 47 161-271 (1919).

75

P. Fatou, ``Sur les équations fonctionelles (deuxieme mémoire),'' Bulletin de la Societe Mathematique de France 48 33-94 (1920).

76

P. Fatou, ``Sur les équations fonctionelles (troisieme mémoire),'' Bulletin de la Societe Mathematique de France 48 208-314 (1920).

43

G. A. Hedlund, ``Endomorphisms and automorphisms of the shift dynamical system,'' Mathematical Systems Theory 3 320-375 (1969).

44

David Hillman ``The structure of reversible one-dimensional automata,'' Physica D 52 277-292 (1991).

45

Jarkko Kari, ``Reversibility and Surjectivity Problems of Cellullar Automata,'' Journal of Computer and System Sciences 48 149-182 (1994).

46

Jarkko Kari, ``Representation of Reversible Cellular Automata with Block Permutations,'' Mathematical Systems Theory 29 47-61 (1996).

47

D. Koenig, Theorie der endlichen und unendlichen Graphen, Akademische Verlagsgesellschaft, Leipzig, 1936. Reprint: Chelsea Publishing Company, New York.

48

Douglas Lind and Brian Marcus, An Introduction to Symbolic Dynamics and Coding, Cambridge University Press, Cambridge, 1995. (ISBN 0-521-55124-2 hardback).

49

Masakazu Nasu, ``Local Maps Inducing Surjective Global Maps of One Dimensional Tessellation Automata,'' Mathematical Systems Theory 11 327-351 (1978).

50

Stephen Wolfram, ``Statistical mechanics of cellular automata,'' Reviews of Modern Physics 55 601-644 (1983).

51

Stephen Wolfram, ``Universality and complexity in cellular automata,'' Physica 10D 1-35 (1984).

52

Stephen Wolfram, ``Computation theory of cellular automata,'' Communications in Mathematical Physics 96 15-57 (1984).

53

Stephen Wolfram (Ed.), Theory and Applications of Cellular Automata, World Scientific Press, Singapore, 1986 (ISBN 9971-50-124-4 pbk).

Chaté-Manneville

54

Bernard Barral, Hugues Chaté and Paul Manneville, ``Collective behaviors in a family of high-dimensional automata,'' Physics Letters A 163 279-285 (1992).

55

R. Bidaux, N. Boccara, and H. Chaté, ``Order of the transition versus space dimension in a family of cellular automata,'' Physical Review A 39 3094-3105 (1989).

81

Jan Hemmingsson, ``A totalistic three-dimensional cellular automaton with quasiperiodic behaviour,'' Physica A 183 255-261 (1992).

57

J. Hemmingsson, A. Sørenson, H. Flyvbjerg and H. J. Herrmann, ``What Synchronization?'' Europhysics Letters 23 629-634 (1993).

71

H. Chaté and P. Manneville, ``Evidence of Collective Behaviour in Cellular Automata,'' Europhysics Letters 14 409-413 (1991).

59

Hugues Chaté and Paul Manneville, ``Collective Behaviors in Spatially Extended Systems with Local Interactions and Synchronous Updating,'' Progress in Theoretical Physics 87 1-60 (1991).

69

H. Chaté, A. Lemaître, Ph. Marcq, P. Manneville, ``Non-trivial collective behavior in extensively-chaotic dynamical systems: an update,'' Physica A 224 447-457 (1996).

70

Hugues Chaté, Jérôme Losson, ``Non-trivial collective behavior in coupled map lattices: A transfer operator perspective,'' Physica D 103 51-72 (1997).

62

Charles H. Bennett, G. Grinstein, Yu He, C. Jayaprakash and David Mukamel, ``Stability of temporally periodic states of classical many body systems,'' Physical Review A 41 1932-1935 (1990).

63

Roger Bideaux, Nini Boccara and Hugues Chaté, ``Order of transition versus space dimension in a family of cellular automata,'' Physical Review A 39 3094-3105 (1989).

64

P. -M. Binder and V. Privman, ``Second-Order Dynamics in the Collective Temporal Evolution of Complex Systems,'' Physical Review Letters 68 3830-3833 (1992).

65

P. -M. Binder, ``Domains and synchronization in high-dimensional cellular automata,'' Physical Review E 51 R839-R840 (1995).

66

Tomas Bohr, G. Grinstein, Yu He, and C. Jayaprakash, ``Coherence, Chaos, and Broken Symmetry in Classical, Many-Body Dynamical Systems,'' Physical Review Letters 58 2155-2158 (1987).

67

Hugues Chaté, ``On the analysis of spatiotemporally chaotic data,'' Physica D 86 238-247 (1995).

68

Hugues Chaté, G. Grinstein and Lei-Han Tang, ``Long-Range Correlations in Systems with Coherent (Quasi)periodic Oscillations,'' Physical Review Letters 74 912-915 (1995).

69

H. Chaté, A. Lemaître, Ph. Marcq, P. Manneville, ``Non-trivial collective behavior in extensively-chaotic dynamical systems: an update,'' Physica A 224 447-457 (1996).

70

Hugues Chaté, Jérôme Losson, ``Non-trivial collective behavior in coupled map lattices: A transfer operator perspective,'' Physica D 103 51-72 (1997).

71

H. Chaté and P. Manneville, ``Evidence of Collective Behaviour in Cellular Automata,'' Europhysics Letters 14 409-413 (1991).

72

Hugues Chaté and Paul Manneville, ``Collective Behaviors in Spatially Extended Systems with Local Interactions and Synchronous Updating,'' Progress of Theoretical Physics 87 1-60 (1991).

73

Hugues Chaté and Paul Manneville, ``Emergence of Effective Low-Dimensional Dynamics in the Macroscopic Behaviour of Coupled Map Lattices,'' Europhysics Letters 17 291-296 (1992).

74

P. Fatou, ``Sur les équations fonctionelles (premiere mémoire),'' Bulletin de la Societe Mathematique de France 47 161-271 (1919).

75

P. Fatou, ``Sur les équations fonctionelles (deuxieme mémoire),'' Bulletin de la Societe Mathematique de France 48 33-94 (1920).

76

P. Fatou, ``Sur les équations fonctionelles (troisieme mémoire),'' Bulletin de la Societe Mathematique de France 48 208-314 (1920).

77

J. A. C. Gallas, P. Grassberger, H.J. Herrmann and P. Ueberholz, ``Noisy collective behaviour in deterministic cellular automata,'' Physica A 180 19-41 (1992).

78

J. Gorodkin, A. Sørensen, and O. Winther, ``Neural Networks and Cellular Automaton Complexity,'' Complex Systems 7 1-24 (1994).

79

G. Grinstein, ``Stability of Nonstationary States of Many-Body Dynamical Systems,'' Journal of Statistical Physics 5 803-815 (1988).

80

Jens M. Houlrick, Itzhak Webman and Mogens H. Jensen, ``Mean field theory and critical behavior of coupled map lattices,'' Physical Review A 41 4210-4222 (1990).

81

Jan Hemmingsson, ``A totalistic three-dimensional cellular automaton with quasiperiodic behaviour,'' Physica A 183 255-261 (1992).

82

J. Hemmingsson and J. Herrmann, ``On Oscillations in Cellular Automata,'' Europhysics Letters 23 15-19 (1993).

83

F. Jiménez-Morales and J. J. Luque, ``Collective behavior of a probabilistic cellular automaton with two absorbing phases,'' Physics Letters A 181 33-38 (1993).

84

Anaël Lemaître, Hugues Chaté, and Paul Manneville, ``Cluster Expansion for Collective Behavior in Discrete-Space Dynamical Systems,'' Physical Review Letters 77 486-489 (1996).

85

Jérôme Losson and Michael C. Mackey, ``Coupled map lattices as models of deterministic and stochastic differential delay equations,'' Physical Review E 52 115-128 (1995).

86

Arkady S. Pikovsky and Jürgen Kurths, ``Do Globally Coupled Maps Really Violate the Law of Large Numbers?'' Physical Review Letters 72 1644-1646 (1994).

87

Y. Pomeau, ``Periodic Behavior of Cellular Automata,'' Journal of Statistical Physics 70 1379-1382 (1993).

Rule 110

88

Matthew Cook, ``Introduction to the activity of rule 110'' (copyright 1994-1998 Matthew Cook) http://w3.datanet.hu/ cook/Workshop/CellAut/
Elementary/Rule110/110pics.html

89

Solomon W. Golomb, Polyominoes Charles Scribner's Sons, New York, 1965.

90

Branko Grünbaum and G. C. Shepard, Tilings and Patterns, W. H. Freeman and Company, New York, 1987 (ISBN 0-7167-1193-1).

91

Wentian Li and Mats G. Nordahl, ``Transient behavior of cellular automaton rule 110,'' Physics Letters A 166 335-339 (1992).

92

Kristian. Lindgren and Mats. G. Nordahl, ``Universal Computation in Simple One-Dimensional Cellular Automata,'' Complex Systems 4 299-318 (1990).

93

Harold V. McIntosh, ``Wolfram's Class IV automata and a good Life,'' Physica D 45 105-121 (1990).

94

Grzegorz Rozenberg and Arto Salomaa, Cornerstones of Undecidability, Prentice Hall, New York, 1994 (ISBN 0-13-297425-8 pbk).

95

W. T. Tutte, Graph Theory As I Have Known It, Clarendon Press, Oxford, 1998 (ISBN 0 19-850251-6).

Lorentz Contraction

96

Serge Lang, 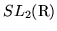$SL_2({\rm R})$, Addison Wesley Publishing Company, Reading, Massachussetts, 1975 (ISBN 0-201-04248-7)

97

V. Bargmann, ``Irreducible unitary representations of the Lorentz group,'' Annals of Mathematics 48 568-640 (1947).

98

E. Wigner, ``On unitary representations of the inhomogeneous Lorentz group,'' Annals of Mathematics 40 149-204 (1939).

Episode I

99

Terry Brooks, Star Wars: Episode I, the Phantom Menace, Ballentine Publishing Company, 1999 (ISBN 0-345-42765-3).

100

David West Reynolds, Star Wars: Episode I, the Visual Dictionary, D. K. Publishing Inc., New York, 1999 (ISBN 0-7894-4701-0).