



Next: Bibliography
Up: Margenes periódicos en la
Previous: Glider H con velocidad
Contents
La estructura periódica que define el ether un T3 beta, puede ordenar las estructuras periódicas con dos números 3 y 4. El ether muestra dos pendientes distintas de desplazamiento, la primera viaja de izquierda a derecha y la segunda en sentido contrario, estos desplazamientos son los que permite el ether en el espacio de evoluciones para cualquier estructura posible.
El desplazamiento del ether que viaja de izquierda a derecha tiene una velocidad de 2/3 ya que se desplaza 2 células a la derecha en 3 generaciones, esto implica que no puede existir una velocidad mayor a 2/3 que viaje de izquierda a derecha en el espacio de evoluciones, porque el margen periódico que existe entre uno y otro T3 es igual a 3, por lo tanto toda estructura o fragmento de estructura tendrá un desplazamiento menor o igual a 2/3.
En el caso contrario cuando el ether se dezplaza de derecha a izquierda, el ether se desplaza 2 células a la izquierda en 4 generaciones, de esta manera la velocidad máxima que puede tener una estructura o fragmento de estructura que viaje de derecha a izquierda es menor o igual a 1/2, en este caso el margen periódico que existe en el ether es igual a 4.
Entonces se puede decir que:
- 1.
- Toda estructura que se desplaza de izquierda a derecha, tendrá una velocidad menor o igual que 2/3.
- 2.
- Toda estructura que se desplaza de derecha a izquierda, tendrá una velocidad menor o igual que 1/2.
- 3.
- Toda estructura que se desplaza de izquierda a derecha, avanzará con incrementos de 2/3 y retrocederá con decrementos de 1/2.
- 4.
- Toda estructura que se desplaza de derecha a izquierda, avanzará con incrementos de 1/2 y retrodecerá con decrementos de 2/3.
- 5.
- Toda estructura que se desplaza de izquierda a derecha, puede ser afectada por otra estructura que se desplaza en sentido contrario, solo si la primera tiene al menos un margen periódico impar y la segunda tiene al menos un margen periódico par.
- 6.
- Toda estructura que se desplaza de derecha a izquierda, puede ser afectada por otra estructura que se desplaza en sentido contrario, solo si la primera tiene al menos un margen periódico par y la segunda tiene al menos un margen periódico impar.
- 7.
- Toda estructura periódica se desplazará hacia adelante o hacia atras 2 células en el espacio de evoluciones por cada margen par o impar que tenga la estructura. Por lo tanto el desplazamiento esta derminado por:
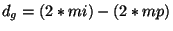 |
(1) |
donde 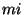 representa el número de margenes impares y
representa el número de margenes impares y 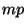 el número de margenes pares y
el número de margenes pares y 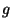 una estructura dada.
una estructura dada.
- 8.
- Toda estructura periódica tendrá un periódo definido por la cantidad de margenes pares e impares, por lo tanto el periódo de una estructura en particular esta derminado por:
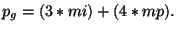 |
(2) |
- 9.
- Entonces una estructura periódica tendrá una velocidad determinada por:
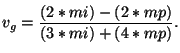 |
(3) |
Finalmente el número de margenes periódicos pares e impares tienen una correspondencia biyectiva respectivamente en cualquier estructura que exista en el espacio de evoluciones.
Se puede ver que para toda estructura que existe en el espacio de evoluciones, si tiene al menos un margen periódico izquierdo impar entonces existe el mismo número de margenes derechos impares. Por otro lado, si tiene al menos un margen izquierdo periódico par entonces existe el mismo número de margenes izquierdos pares.
- (a)
- Para toda estructura que se desplaza de izquierda a derecha, si tiene al menos un margen periódico par izquierdo, entonces implica que tiene
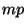 puntos de contacto a la izquierda y
puntos de contacto a la izquierda y 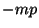 puntos que no son de contacto del lado derecho.
puntos que no son de contacto del lado derecho.
- (b)
- Para toda estructura que se desplaza de derecha a izquierda, si tiene al menos un margen periódico impar derecho, entonces implica que tiene
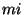 puntos de contacto a la derecha y
puntos de contacto a la derecha y 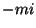 puntos que no son de contacto del lado izquierdo.
puntos que no son de contacto del lado izquierdo.
- (c)
- Para cada
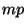 y
y 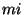 que existan en un margen dado, implica la existencia de su contraimagen en el margen opuesto.
que existan en un margen dado, implica la existencia de su contraimagen en el margen opuesto.
Tabla 1:
Margenes y velocidades de los gliders
| |
margenes |
|
| estructura |
izquierdo - derecho |
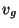 |
| |
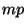 |
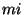 |
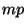 |
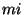 |
|
| ether izquierda |
. |
1 |
. |
1 |
2/3 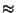 0.666 0.666 |
| ether derecha |
1 |
. |
1 |
. |
-1/2 = -0.5 |
| A |
. |
1 |
. |
1 |
2/3 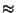 0.666 0.666 |
| B |
1 |
. |
1 |
. |
-1/2 = -0.5 |
| Bbar |
3 |
. |
3 |
. |
-1/2 = -0.5 |
| Bbar8 |
3 |
. |
3 |
. |
-1/2 = -0.5 |
| C1 |
1 |
1 |
1 |
1 |
0 |
| C2 |
1 |
1 |
1 |
1 |
0 |
| C3 |
1 |
1 |
1 |
1 |
0 |
| D1 |
1 |
2 |
1 |
2 |
1/5 = 0.2 |
| D2 |
1 |
2 |
1 |
2 |
1/5 = 0.2 |
| E |
3 |
1 |
3 |
1 |
-4/15 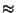 -0.266 -0.266 |
| Ebar |
6 |
2 |
6 |
2 |
-4/15 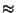 -0.266 -0.266 |
| F |
6 |
4 |
6 |
4 |
-1/9 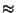 -0.111 -0.111 |
| G |
9 |
2 |
9 |
2 |
-1/3 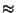 -0.333 -0.333 |
| H |
17 |
8 |
17 |
8 |
-9/46 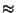 -0.195 -0.195 |
|
Aplicando la ecuación de velocidad determinada por los margenes periódicos y los desplazamientos de orden par tenemos por ejemplo:
- Para el glider A,
- Para el glider C1,
- Para el glider H,
Las margenes periódicos 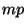 y
y 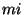 siempre tendran una altura de 4 y 3 respectivamente.
siempre tendran una altura de 4 y 3 respectivamente.




Next: Bibliography
Up: Margenes periódicos en la
Previous: Glider H con velocidad
Contents
ice
2002-03-11
![]() representa el número de margenes impares y
representa el número de margenes impares y ![]() el número de margenes pares y
el número de margenes pares y ![]() una estructura dada.
una estructura dada.
![]() representa el número de margenes impares y
representa el número de margenes impares y ![]() el número de margenes pares y
el número de margenes pares y ![]() una estructura dada.
una estructura dada.
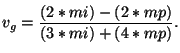
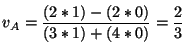
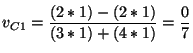
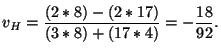
![]() y
y ![]() siempre tendran una altura de 4 y 3 respectivamente.
siempre tendran una altura de 4 y 3 respectivamente.