![]()
Dentro de los autómatas celulares existen ciertas condiciones de evolución, las cuales presentan la característica de que esta evolución puede ser seguida a través del tiempo de la manera más común, esto es decir, una nueva célula se obtiene a través de sus ancestores, pero con la característica de que esta nueva célula puede dar origen a sus ancestros a través de otra regla llamada regla reversible, esta sigue una evolución por las mismas configuraciones que esta formo en su trayectoria anterior hasta llegar a la configuración inicial original. Existen grados de reversibilidad dependiendo de las configuraciones tomadas en cuenta, los hay arbitrarios, periódicos o tranquilos en el infinito. Los autómatas celulares son sistemas dinámicos abstractos que juegan un papel en las matemáticas discretas comparable al que juegan las ecuaciones diferenciales en las matemáticas continuas. Hace pocos años el conocimiento sobre autómatas reversibles ( Invertible Celular Automata ICA) podía ser expresado en unas cuantas líneas (y no era muy interesante tampoco), ahora uno puede decir una historia más interesante, y nosotros tenemos que intentar hacer este papel también. La relación con ICA representa el resultado de varios aáos de investigación que incluyen:
Una asignación de estados a todas las células, un estado para un autómata celular entero, es llamado una configuración. Con la aplicación de un mapeo local a todas las celdas de la cadena de cualquier configuración q, obteniendo una nueva configuración q', la cual es llamada sucesor así el mapeo local define una transformación
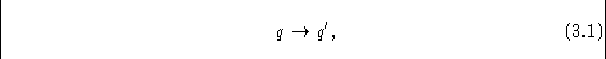
llamada mapeo global, sobre el conjunto de configuraciones. Un Autómata Celular es
reversible si su mapeo es reversible, por ejemplo si cualquier configuración, la cual por
definición, tiene exactamente un sucesor también un predecesor.
En 1962, Moore preguntó si podrían existir configuraciones de "Jardines de
Edén" -configuraciones que no tienen predecesor- y probó que bajo ciertas
condiciones, si una configuración tiene más de un predecesor entonces debería haber
alguna que no tenga ninguno.
Fredkin ha estado estudiando recursos de invertibilidad como modelos de comportamiento dinámico. A llegado a técnicas para la arbitraria sintetización secuencial de comportamientos booleanos invertibles; y tiene estudios de una clase de ICA que muestran algunas analogías con mecanismos de Lagrange.
![]()