![]()
En la matriz de evolución se ve que el elemento (0,0) evoluciona en uno, por lo tanto, el producto tensorial multiplicará el elemento (0,0) de la matriz de conectividad con la matriz B (evolución en el estado 1) y de esta forma se obtiene su submatriz de conectividad:
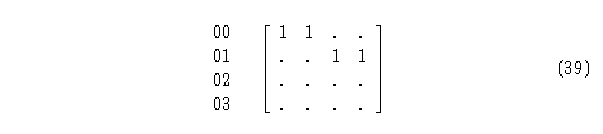
la cual pertenece a la matriz asociada del diagrama de Parejas.
Esta submatriz es estocástica por columna, la matriz de parejas es una herramienta eficaz para observar el número de ancestros de una configuración, también se puede observar que existe una propiedad de simetría como se ve a continuación:
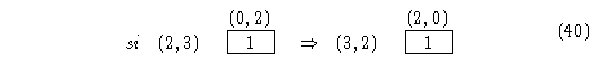
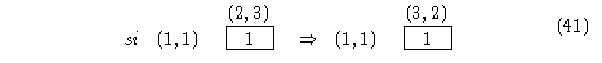
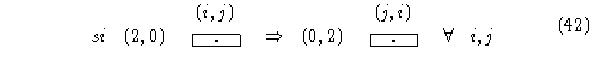
por lo tanto, se puede generalizar,
si (x,y) conecta a (x',y') entonces (y,x) conecta a (y',x')
El diagrama de Parejas describe las relaciones de parejas ordenadas; pero su propiedad de simetría nos permite obtener un diagrama desordenado, en el cual la distinción entre (x,y) y (y,x) se considera insignificante. De esta manera se produce un diagrama más pequeño, éste puede observarse uniendo los nodos correspondientes del diagrama de Parejas original.
Seck Tuoh Mora Juan Carlos
E-mail:seck@delta.cs.cinvestav.mx