![]()
El uso de estas matrices es una alternativa para obtener la regla inversa de un autómata (4,h). Dentro de las matrices de conectividad del diagrama de de Bruijn para autómatas con r=h, se observa una propiedad que indica si es reversible. Esta es que el número de nodos del diagrama de de Bruijn, es igual a la máxima suma por renglones multiplicada por la máxima suma por columnas. Tomemos las matrices de conectividad del diagrama de de Bruijn de un autómata (4,h), regla 05AF0FA5.
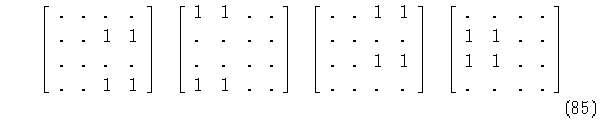
Por ejemplo, sea
![]()
cualquier elemento de la matriz A, entonces tenemos que:
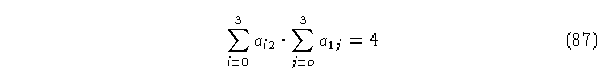
para el caso de un ACLR(4,h)donde la suma máxima por renglón y por columna se
denominan índices de Welch. Utilizando las matrices de conectividad anteriormente dadas,
se obtendrá su regla inversa para este autómata.
Algoritmo para obtener la regla inversa
a) Tomar una vecindad para la cual se desee conocer el elemento con el que evoluciona
en el pasado.
b) Del primer elemento de la vecindad, tomar su matriz de conectividad y de ahí
obtener los elementos cuya suma por columna sea diferente de cero.
c) Del segundo elemento de la vecindad, tomar su matriz de conectividad y de ahí
obtener los elementos cuya suma por renglón sean diferente de cero.
d) De los elementos obtenidos en b) y c), tomar el elemento que se intersecta.
e) De la vecindad tomada en a), especificar su evolución en el pasado como el elemento
en común obtenido en d).
f) Repetir los pasos anteriores para cada una de las vecindades.
Esta característica sólo se da para los ACLR con radio de vecindad h, tomando
nuevamente el autómata (4,h), regla 05AF0FA5.
Regla de evolución :
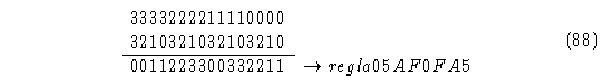
Algoritmo:
a) Se toma la vecindad 01.
b) Matriz del elemento 0.
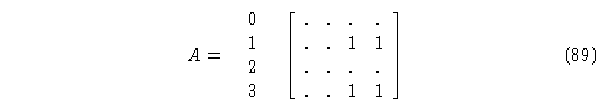
Columnas con suma de elementos diferentes de cero: 2 y 3.
c) Matriz del elemento 1.
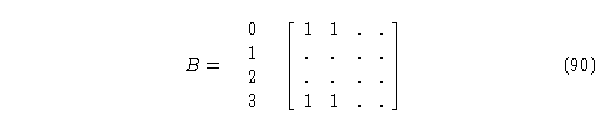
Renglones con suma de elementos diferentes de cero: 0 y 3.
![]()
![]()
De este modo las matrices de conectividad de la regla inversa quedarán de la siguiente manera:
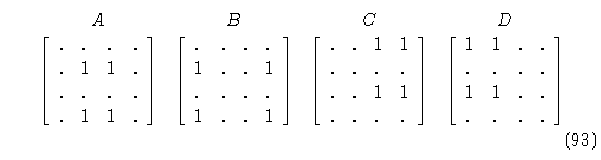
de estas matrices de conectividad se obtiene la regla inversa.
Regla inversa.
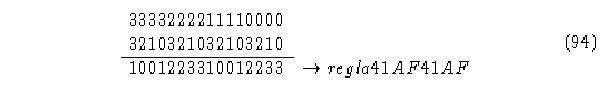
Justamente la misma regla que se había obtenido por el modelo de Fredkin para este autómata.
![]()
Seck Tuoh Mora Juan Carlos
E-mail:seck@delta.cs.cinvestav.mx