![]()
Un Autómata Celular Lineal es un mecanismo capaz de realizar una serie de acciones
independientes. Cada parte del mecanismo puede decidir su propio accionar a partir de su
entorno local.
Este mecanismo consiste en una serie de celdas (células) conectadas en linea, como lo muestra la figura 1.
La línea de células puede considerarse como cerrada por la frontera, donde la última
célula se conecta con la primera, dando la forma de un anillo.
Cada parte del mecanismo puede tomar diferentes valores, tales valores pueden
representar una acción o una característica en especial, para fines de generalidad estos
se representan con los primeros enteros: 0,1,2,3..
Cada una de las células en toda la línea cambia su estado a través del tiempo. Dicho cambio depende de su entorno local, es decir, de los valores que tenga la célula en cuestión y los vecinos más cercanos que hayan sido convenidos para formar el entorno o vecindad (fig. 2).
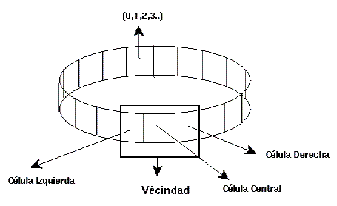
Figura 2: Vecindades y estados de un A.C.
Las configuraciones que van resultando del cambio de valores de las células en toda la
línea a través del tiempo se les conoce como generaciones y al conjunto de todas estas
generaciones es llamado la evolución de un A.C. (fig. 3).
Suponga que se tiene una vecindad de tres elementos, es decir un entorno local donde la
interacción de tres elementos decide el valor de las células, en la siguiente
generación. Y suponga que los valores que puede tener cada célula son dos:0,1. Esto dá
un total de 8 posibles vecindades que se pueden presentar con la combinación de estos
estados en las tres células.
Si a cada vecindad se le asigna el valor resultado de la interación de los elementos que
lo componen se tiene lo que se denomina como la regla de evolución del A.C..
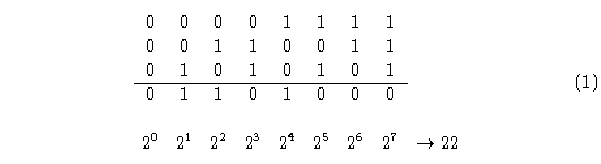
Cada regla puede tener un nombre con la nomenclatura de Wolfram que consiste en tomar el número de la regla como binario haciendo la lectura de izquierda derecha y calcularle el decimal correspondiente. Entonces el número binario de nuestra regla es 0110100 y su decimal 22.
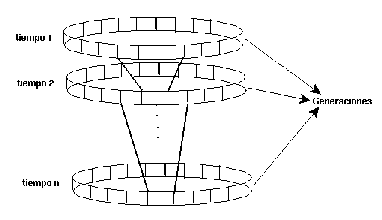
Figura 3: Evolución de un A.C.
Para ver la evolución de un A.C. se necesitan dos cosas:
Un A.C. es un modelo que cambia con respecto al tiempo de manera discreta, por lo que se le reconoce como un sistema dinámico discreto.
De manera general se pueden reconocer las siguientes características de un A.C.:
Una vez determinado en número de estados y el tamaño de la vecindad, el siguiente
paso es estudiar la evolución del A.C..
La evolución representa en primer término una descripción visual del comportamiento
del A.C.
Sin embargo ver la evolución de un A.C. no es suficiente para poder determinar de una
manera rigurosa las características de su comportamiento. Existe mucha ambigüedad en la
apreciación de patrones: las semejanzas son tan aparentes como las diferencias.
Debido a lo anterior existe un esfuerzo por caracterizar a un A.C. por medio de
herramienta matemática que ayude a determinar con mayor exactitud su comportamiento. Este
esfuerzo se ha encaminado sobre dos grandes lineas de investigación las cuales se
describen en la siguiente sección.
![]()