![]()
Para definir a los diagramas de subconjuntos podemos comenzar por darnos cuenta de que
de las ligas son supuestas diferentes clases, dentro de estas pueden contener conectividad
individual en una representación matricial, aislados de distintas direcciones en el
diagrama, estas etiquetas siguen cierta secuencia, los nodos son agrupados dentro dentro
de subconjuntos, el resultado es una nueva gráfica, con subconjuntos para nodos y
conexiones reduciendo todos los sitios que que uno puede obtener de todas las posibles
combinaciones, esto es catalogado en cualquier evento. Otra importante razón para
trabajar con diagramas de subconjuntos es que las conexiones etiquetadas son parecidas a
funciones, por asociación de una cosa por otra, pero si dos conexiones con etiquetas
parecidas surgen de un solo vértice, dificilmente pueden ser funciones.
Una vez que los diagramas han sido formados, si las direcciones primeras del conjunto
universal a el conjunto vacio, y determina si solo existe direcciones para una sola clase,
las direcciones semejantes, si existen, podrían ser usadas por fuerza dentro de un
autómata a un estado predeterminado, ahora esta es la parte que contiene la condición
inicial. representamos ahora el la manera en que se crean las clases de subconjuntos,
poteriormente el diagrama de subconjuntos del autómata celular anterior.
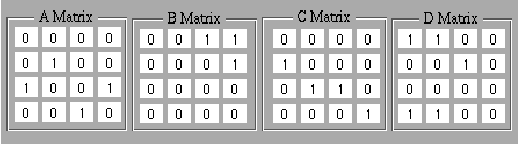
Figura 3.3: Diagrama de conjuntos para un Autómata Celular (4,h),
regla 8F28725F.