![]()
El diagrama de de Bruijn nos da la oportunidad de trazar rutas en él y verificar que
estados las originan, sin embargo una pregunta importante es saber si una ruta dada existe
o es posible de construir en el diagrama [14]; para
responder ésto se ha utilizado el diagrama de Subconjuntos desarrollado por Moore
[15] el cual toma como base al diagrama de de Bruijn; los
nodos son agrupados en subconjuntos que van desde el conjunto vacío, los subconjuntos de
nodos unitarios, los subconjuntos de parejas distintas de nodos hasta el subconjunto que
contenga todos los nodos; si el diagrama de de Bruijn tiene n nodos el diagrama de
subconjuntos tendrá ![]() nodos, veamos el caso para
un ACL(2,1) regla 22.
nodos, veamos el caso para
un ACL(2,1) regla 22.
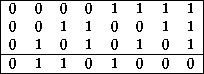
Tabla: Regla de evolución 22 del ACL(2,1).
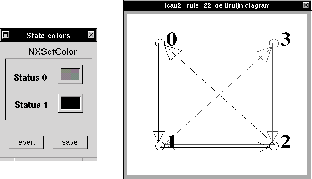
Figura: Diagrama de de Bruijn de un ACL(2,1) regla 22.
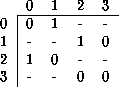
Tabla: Matriz de evolución del ACL(2,1) regla 22.
El diagrama de subconjuntos tendrá ![]() nodos que
se enumerarán desde el 0 para el conjunto vacío hasta el 15 para el subconjunto
total utilizando una notación binaria, es decir si tenemos 4 nodos se ordenan 0,1,2,3;
si el subconjunto lo forman los nodos
nodos que
se enumerarán desde el 0 para el conjunto vacío hasta el 15 para el subconjunto
total utilizando una notación binaria, es decir si tenemos 4 nodos se ordenan 0,1,2,3;
si el subconjunto lo forman los nodos ![]() en la
secuencia de nodos tendríamos 0,1,1,0 donde el 0 significa la ausencia del
nodo y el 1 la presencia del mismo, con ésto el subconjunto
en la
secuencia de nodos tendríamos 0,1,1,0 donde el 0 significa la ausencia del
nodo y el 1 la presencia del mismo, con ésto el subconjunto ![]() le corresponde el valor 6 y así para todos los casos.
le corresponde el valor 6 y así para todos los casos.
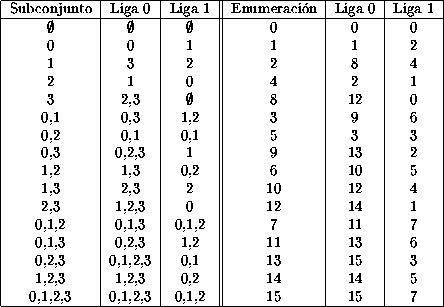
Tabla: Subconjuntos del diagrama de de Bruijn del ACL(2,1) regla 22.
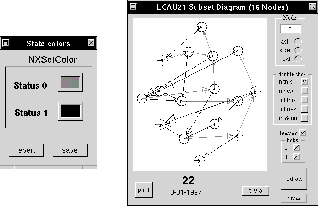
Figura: Diagrama de Subconjuntos de un ACL(2,1) regla 22.
Varias observaciones sobre la construcción del diagrama de subconjuntos son:
A) El conjunto vacío liga a sí mismo con cualquier liga.
B) Existe una liga del nodo a al nodo b si al menos un elemento del
nodo a tiene enlace por medio de esa liga al nodo b, no importando que los
demás elementos carezcan de tal conexión.
Otra importante razón para utilizar el diagrama de subconjuntos es que proporciona una funcionalidad que posiblemente no exista en el diagrama de de Bruijn ya que en este último dos ligas del mismo color pueden partir de un mismo nodo cosa que no ocurre en el diagrama de subconjuntos, donde cada nodo tiene una sola liga correspondiente a cada estado del ACL, el conjunto vacío asegura que en cada nodo todas las ligas estén definidas para todos los estados del autómata, la matriz de adyacencia del diagrama de subconjuntos para el ACL(2,1) regla 22 agrupando los subconjuntos de acuerdo a su tamaño es como sigue:

Tabla: Matriz del diagrama de subconjuntos del ACL(2,1) regla 22.
![]()