![]()
La parte central del estudio de un ACLR es su regla de evolución, ya que ésta nos dice como se comporta el sistema a través del tiempo, lo interesante es que esta regla de evolución es de influencia local, o sea solo afecta las vecindades que forman parte de la configuración, sin embargo tal regla induce un mapeo global el cual es reversible.
Desde esta perspectiva podemos tomar a la evolución como una función que escencialmente transforma elementos de un conjunto a otro, donde tales elementos son las configuraciones globales que puede tener el ACL y la función el mapeo global producto de la regla de evolución.
Las funciones se pueden clasificar por el mapeo que producen obteniendo las siguientes definiciones [19]:
Una función ![]() se dice
se dice
En [19] se describe claramente estos conceptos en los siguientes diagramas:
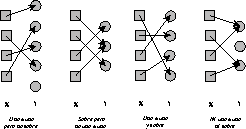
Figura: Diferentes tipos de mapeo de una función.
Si un mapeo ![]() es
biyectivo, entonces
es
biyectivo, entonces ![]() también define una función biyectiva; por lo tanto, caracterizar a los ACLR es encontrar
que propiedades debe tener el mapeo inducido por la regla de evolución para que éste sea
biyectivo, sabiendo además que existe una regla inversa a la original.
también define una función biyectiva; por lo tanto, caracterizar a los ACLR es encontrar
que propiedades debe tener el mapeo inducido por la regla de evolución para que éste sea
biyectivo, sabiendo además que existe una regla inversa a la original.
Usando un poco de nomenclatura de estructuras algebraicas podemos decir que el mapeo global define un homomorfismo de X a X, como el dominio como el contradominio de la función es el mismo, ésta es un endomorfismo y ya que tal función debe ser biyectiva (uno a uno y sobre) para que el ACL sea reversible, esta función debe definir un automorfismo.
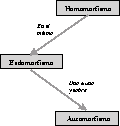
Figura: La regla de evolución de un ACLR define un automorfismo.
Tomando como base el trabajo de [9] y [16] se expondrán tres definiciones que exponen estos autores para caracterizar la regla de evolución de un ACLR, los cuales son Multiplicidad Uniforme, Indices de Welch y Combinabilidad.
La sección 5 en [9] demuestra que el mapeo global inducido por un ACL es sobreyectivo si y solo si cada mapeo menor contenido en éste es sobreyectivo y además, el número de ancestros de cada uno de éstos mapeos es igual al número de nodos en el diagrama de de Bruijn (multiplicidad), siendo este número igual para cada posible configuración (uniformidad), ilustremos este concepto con un ACLR(5,h).
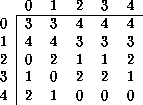
Tabla: Regla de evolución 0077A76AIJOOI de un ACLR(5,h).
Las configuraciones que pueden formar la cadena 0 son:
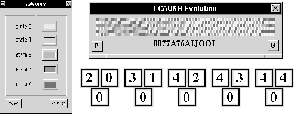
Figura: Configuraciones de tamaño 2 que evolucionan en 0.
Definamos ahora las configuraciones que evolucionan en la cadena 02.
![]()
Figura: Configuraciones de tamaño 3 que evolucionan en 02.
Podemos hacer cada vez mas grandes estas cadenas y seguiremos encontrando que el
número de ancestros de cada una de éstas es el mismo, definamos como ![]() ={421,424,432,433,440} al conjunto de
configuraciones que son ancestros de 02 con
={421,424,432,433,440} al conjunto de
configuraciones que son ancestros de 02 con ![]() , definamos como
, definamos como ![]() ={0,1,2,3,4} al conjunto de estados del ACL con
={0,1,2,3,4} al conjunto de estados del ACL con ![]() y
y ![]() al conjunto de ancestros de una cadena
al conjunto de ancestros de una cadena ![]() , entonces tenemos que
, entonces tenemos que ![]() .
.

Figura: Conjunto de ancestros de las configuraciones ![]() .
.
Tenemos que ![]() ; supongamos
que
; supongamos
que ![]() para todo
para todo ![]() , si existe
, si existe ![]() para cualquier
para cualquier ![]() , tendriamos que
, tendriamos que ![]() lo que no es posible, por lo tanto se concluye
que
lo que no es posible, por lo tanto se concluye
que ![]() para cada
para cada ![]() , este resultado se extiende
para cualquier cadena y las extensiones que se hagan a la misma.
, este resultado se extiende
para cualquier cadena y las extensiones que se hagan a la misma.
Encontremos ahora cual es el valor que toma a para cada caso; tomemos ![]() {421,424,432,433,440} con
{421,424,432,433,440} con ![]() ,
, ![]() ={0,1,2,3,4} al conjunto de configuraciones de
tamaño 2r con
={0,1,2,3,4} al conjunto de configuraciones de
tamaño 2r con ![]() , si
tomamos la cadena 02
, si
tomamos la cadena 02![]() 02
tenemos que
02
tenemos que ![]() ya que al
hacer cada posible concatenación de 2 cadenas del conjunto
ya que al
hacer cada posible concatenación de 2 cadenas del conjunto ![]() obtenemos toda posible instancia de la cadena 02
obtenemos toda posible instancia de la cadena 02![]() 02, entonces
02, entonces ![]() , tomemos ahora un elemento
del conjunto
, tomemos ahora un elemento
del conjunto ![]() , (el 1 en
este caso aunque puede ser cualquier elemento) y formemos la cadena 02102 con todos sus
posibles ancestros.
, (el 1 en
este caso aunque puede ser cualquier elemento) y formemos la cadena 02102 con todos sus
posibles ancestros.
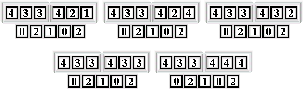
Figura: Elementos del conjunto ![]() de cadenas que evolucionan en 02 que forman los ancestros
de la configuración 02102.
de cadenas que evolucionan en 02 que forman los ancestros
de la configuración 02102.
Tenemos que ![]() lo que
ocurre para cada posible elemento de
lo que
ocurre para cada posible elemento de ![]() , ya que
, ya que ![]() ,
tenemos que
,
tenemos que ![]() , de este
modo a=k; sabemos que k está dada por el número de configuraciones
diferentes de tamaño 2r que es la misma manera en que se definen los nodos en el
diagrama de de Bruijn, por lo tanto se concluye que en un ACL con un mapeo global
sobreyectivo cada cadena de estados debe tener tantos ancestros como el número de
configuraciones diferentes que se puedan hacer de tamaño 2r o como nodos existan
en su diagrama de de Bruijn correspondiente.
, de este
modo a=k; sabemos que k está dada por el número de configuraciones
diferentes de tamaño 2r que es la misma manera en que se definen los nodos en el
diagrama de de Bruijn, por lo tanto se concluye que en un ACL con un mapeo global
sobreyectivo cada cadena de estados debe tener tantos ancestros como el número de
configuraciones diferentes que se puedan hacer de tamaño 2r o como nodos existan
en su diagrama de de Bruijn correspondiente.
La definición de este concepto se debe a L. R. Welch colaborador de
Hedlund, en la sección 14 en [9] se definen estos
índices como sigue:
Sea A cualquier bloque de estados y ![]() el i-ésimo conjunto de extensiones por la derecha de A
tal que
el i-ésimo conjunto de extensiones por la derecha de A
tal que ![]() evolucionen en la
misma cadena, así definamos
evolucionen en la
misma cadena, así definamos ![]() , entonces se tomará
, entonces se tomará ![]() es decir, la cardinalidad del conjunto
es decir, la cardinalidad del conjunto ![]() con mayor número de elementos; se define de
manera análoga L para
con mayor número de elementos; se define de
manera análoga L para ![]() , las extensiones compatibles por la izquierda de un bloque de estados.
, las extensiones compatibles por la izquierda de un bloque de estados.
Ejemplifiquemos este concepto con un ACL(5,h) reversible.
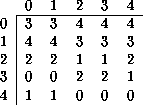
Tabla: Regla de evolución 0067A26CIJOOI de un ACLR(5,h).
Tomemos el estado 0 y busquemos las extensiones a la derecha compatibles con éste tal que la evolución sea 3 ó 4:
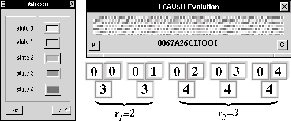
Figura: Regla de evolución 0067A26CIJOOI de un ACLR(5,h), y las
extensiones derechas compatibles con 0 que evolucionan en 3 y 4.
Para este caso R=3 ya ![]() es la cardinalidad del mayor conjunto compatible por la derecha
es la cardinalidad del mayor conjunto compatible por la derecha ![]() de 0, ahora busquemos a
de 0, ahora busquemos a
![]() tal que la evolución se 34
y 40.
tal que la evolución se 34
y 40.

Figura: Extensiones derechas compatibles con 0 que evolucionan en 34
y 40.
Ahora ![]() , si ahora
tomamos
, si ahora
tomamos ![]() compatible por la
derecha tal que la evolución se 342 tenemos:
compatible por la
derecha tal que la evolución se 342 tenemos:
![]()
Figura: Extensiones derechas compatibles con 0 que evolucionan en 342.
Podemos continuar de forma indefinida incrementado cada vez más las extensiones compatibles por la derecha del estado 0 y encontraremos que R se mantendrá con valor 5 para este ACL, lo mismo ocurre para todas las extensiones derechas de los demás estados.
Ahora busquemos ![]() compatible por la izquierda del mismo estado 0 tal que la evolución sea 3 y
4 y observemos lo que se obtiene:
compatible por la izquierda del mismo estado 0 tal que la evolución sea 3 y
4 y observemos lo que se obtiene:
![]()
Figura: Extensiones izquierdas compatibles con 0 que evolucionan
en 3 y 4.
En este caso ![]() , si
extendemos la evolución a 23 ó 14 resulta:
, si
extendemos la evolución a 23 ó 14 resulta:
![]()
Figura: Extensiones izquierdas compatibles con 0 que evolucionan
en 23 y 14.
Se observa que L sigue siendo 1. Definamos ahora A como un bloque de
estados y ![]() como el
conjunto de bloques de estados A en donde las extensiones L y R de
cada
como el
conjunto de bloques de estados A en donde las extensiones L y R de
cada ![]() evolucionen en la
misma cadena bajo la regla de evolución y denotemos a
evolucionen en la
misma cadena bajo la regla de evolución y denotemos a ![]() , tomemos un ejemplo de todas las posibles cadenas
evolucionen en 231.
, tomemos un ejemplo de todas las posibles cadenas
evolucionen en 231.

Figura: Ancestros de la cadena 231.
En este caso M=1 ya que hay un solo elemento en el cual sus extensiones por
derecha y por izquierda interactúen con el para evolucionar en 231, una propiedad
fundamental que Hedlund y Welch postulan es que si un ACL(k,r) define un mapeo global
sobreyectivo, entonces la multiplicación de ![]() o igual al número de nodos en el diagrama de de Bruijn, veamos
como funciona ésto para la cadena de estados 130 y sus posibles ancestros.
o igual al número de nodos en el diagrama de de Bruijn, veamos
como funciona ésto para la cadena de estados 130 y sus posibles ancestros.
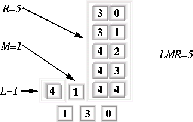
Figura: Ancestros de la cadena 130.
Se observa en este caso que M=1 para esta configuración, ya que el estado 1 y sus conjunto compatibles por la izquierda y derecha son los únicos que evolucionan en la cadena 130, con L=1 y R=5, ilustremos ésto con otros ACLR.
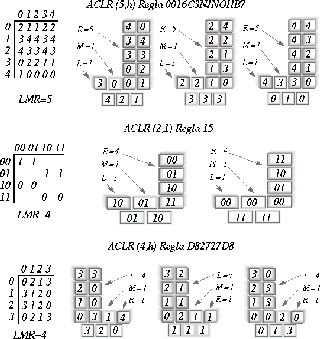
Figura: Ejemplos de ACLR y sus valores de LMR.
Por supuesto, no siempre L ó R deben ser igual a 1, ya que hay casos en
el que el valor ![]() puede ser
formado por otras combinaciones que no contemplen 1; el único caso en el que L ó R
deben ser 1 es cuando el valor de
puede ser
formado por otras combinaciones que no contemplen 1; el único caso en el que L ó R
deben ser 1 es cuando el valor de ![]() es primo, a continuación se presentan algunos ejemplos de ACLR donde este
valor no es primo.
es primo, a continuación se presentan algunos ejemplos de ACLR donde este
valor no es primo.
En la sección 16 de [9] y y en el
trabajo de [16] se define este concepto el cual nos dice
que un mapeo local es debilmente combinable si para toda cadena dada de estados
de longitud l = 2r el conjunto ![]() de sus extensiones compatibles por la derecha debe tener una cardinalidad
igual a R o a 0 y el conjunto
de sus extensiones compatibles por la derecha debe tener una cardinalidad
igual a R o a 0 y el conjunto ![]() de sus extensiones compatibles por la izquierda debe tener una
cardinalidad igual a L o a 0, ilustremos un ejemplo de esta definición
mostrando un ACL(5,h) no reversible.
de sus extensiones compatibles por la izquierda debe tener una
cardinalidad igual a L o a 0, ilustremos un ejemplo de esta definición
mostrando un ACL(5,h) no reversible.
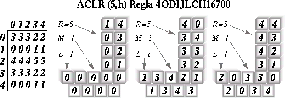
Figura: ACL no reversible (5,h) con cadenas cuyas valores de ![]() .
.
Aquí se observa que este ACL tiene configuraciones con valores de L=1, M=1 y R=5, sin embargo tomemos la cadena formada alternando los estados 0,2 y observemos sus posibles ancestros.
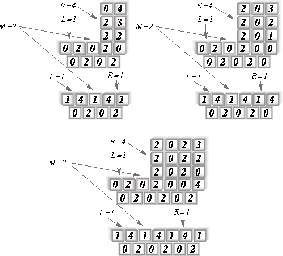
Figura: Ancestros de la cadena formada alternando los estados 0,2.
En este caso una cadena de este tipo puede ser generada por las extensiones compatibles de dos estados distintos, un estado con R=4 y el otro con R=1, es decir, el valor de M=2, por lo que este ACL tiene múltiples ancestros para esta cadena en particular, lo que impide que sea reversible; lo mismo sucede con la cadena formada alternando los estados 1,4.
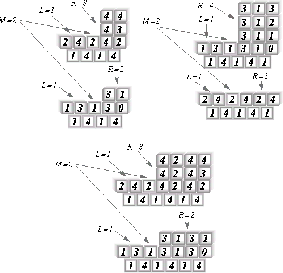
Figura: Ancestros de la cadena formada alternando los estados 1,4.
En un ACLR el valor de M debe ser siempre igual a 1 y los ancestros de
las cadenas de longitud ![]() deben tener índices L y R con
deben tener índices L y R con ![]() , es decir cada posible ancestro de debe estar formado por las
extensiones compatibles de una cadena de estados de longitud l=2r en donde se
cumpla que para el conjunto
, es decir cada posible ancestro de debe estar formado por las
extensiones compatibles de una cadena de estados de longitud l=2r en donde se
cumpla que para el conjunto ![]() de extensiones compatibles por la derecha del mismo,
de extensiones compatibles por la derecha del mismo, ![]() y para el conjunto
y para el conjunto ![]() de extensiones compatibles por la izquierda del
estado,
de extensiones compatibles por la izquierda del
estado, ![]() , tomemos como
ejemplo un ACLR(5,h).
, tomemos como
ejemplo un ACLR(5,h).
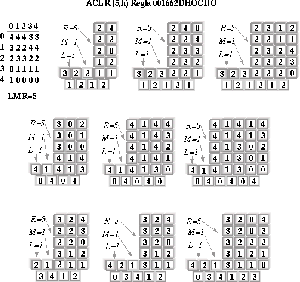
Figura: ACLR(5,h) donde el valor de M siempre es igual a 1.
La propiedad de que la regla de evolución de un ACL sea debilmente combinable obliga a que una cadena de estados sea producto de la evolución de una única cadena de estados de longitud l=2r con sus extensiones compatibles derechas e izquierdas, evitando así que otra secuencia de estados evolucione en la misma cadena y ésta tenga múltiples ancestros.
![]()