Enigma

Con el Tratado de Versalles de 1919 se reconoce en Europa la restitución de Polonia.

Por su posición geográfica entre la U.R.S.S. y Alemania, el Gobierno de la República de Polonia establece una oficina de cifrado, Biuro Szyfrów, con el fin de interceptar las comunicaciones, de radio principalmente (los mensajes cifrados eran comunicados en el código Morse), de los gobiernos de esos países. Sin grandes dificultades, los criptólogos polacos de esa época pudieron descifrar los esquemas criptográficos utilizados. Uno de los principales criptólogos de los años 20 en esa oficina fue el lugarteniente Jan Kowalewski, matemático y lingüista, quien en 1921 fue condecorado luego de la guerra con la URSS y posteriormente fue asesor del Imperio Japonés para criptografía. Entre los matemáticos que entonces participaron en el Biuro Szyfrów estaban Stefan Mazurkiewicz, Wacaw Sierpinski y Stanisaw Lesniewski [11].

En 1926, los polacos notaron un cambio en los métodos usados y llegaron a la conclusión de que se estaba utilizando un procedimiento mecánico para cifrar las comunicaciones alemanas. Era imperativo para la seguridad polaca quebrantar ese método de cifrado.

Hugo Alexander Koch, holandés, y Arthur Scherbius, alemán, fueron los inventores de la máquina Enigma, alrededor de 1923, con el propósito inicial de cifrar, con propósito comercial, las comunicaciones industriales y bancarias. La máquina cifradora llamó poco la atención de esos medios y la fábrica establecida por Scherbius fue liquidada. Sin embargo, los militares alemanes recuperaron ese invento, desde 1925, y fue utilizado hasta 1945 por el ejército de tierra, la marina y la aviación. En los 20 y los 30 hubo en el Mundo varias máquinas cifradoras. En los Estados Unidos de Norteamérica se utilizaba la máquina SIGABA, inventada por William Friedman, y en la Gran Bretaña, TypeX. De hecho, hasta la década de los 70 se seguía utilizando máquinas cifradoras, de rotores.

Enigma se basaba en permutaciones de orden dos, llamadas involuciones, sobre un alfabeto de 26 caracteres. Al ser las involuciones iguales a sus propias inversas, los procesos de cifrado y descifrado coincidían. Así que cuando un texto en claro se aplicaba a una máquina, ésta producía un correspondiente texto cifrado, y cuando el texto cifrado se aplicaba a la misma máquina, ésta producía el correspondiente texto en claro. Por lo cual, dos partes comunicantes debían ponerse de acuerdo en una misma configuración de sus propias máquinas Enigma para poder comunicarse. La configuración era pues la clave de cifrado.

Figura 1: Máquina de cifrado Enigma de tres rotores. (a) Fotografía de una máquina Enigma. (b) Diagrama mostrando las partes principales. Se ilustra oprimiendo $N$ para obtener el cifrado $F$.

(a)	(b)

Descripciones completas del funcionamiento de Enigma aparecen en [5], en [1], en [8] y en los capítulos 5-6 de [2]. En la figura 1 presentamos una fotografía de una máquina Enigma y un diagrama de sus principales componentes. En lo que sigue, haremos solamente un ejercicio de conteo para ilustrar que el espacio de posibles claves es muy, pero muy, grande.

El alfabeto que utilizaban las máquinas Enigma consistía de las 26 letras del alfabeto latino, no incluían ni los dígitos ni los signos de puntuación. Las primeras máquinas Enigma utilizaban un tambor de entrada, tres rotores, un ``reflector'' y un ``tablero de conexiones''. El ``teclado'' de salida era una colección de bulbos que se iban iluminando consecutivamente para mostrar el texto cifrado correspondiente al texto en claro introducido mediante el teclado de entrada.

El tablero de conexiones consistía de 26 empalmes, correspondientes a las letras, los cuales se conectaban a pares por un cierto número de cables, que podía ser entre 0 y 13 inclusive. El número de posibilidades para el tablero de conexiones era pues

$$n_1=\sum_{i=0}^{13}{26 \choose 2i}\prod_ {j=1}^{i-1}(2j+1) = ... ..._{i=0}^{13}\frac{26!}{(26-2i)!i!2^i} = 532\,985\,208\,200\,576.$$

El reflector trabajaba como el tablero de conexiones con exactamente 13 pares de conexiones, por lo que el número de posibilidades era $n_2=\frac{26!}{13!2^{13}} = 7\,905\,853\,580\,625.$

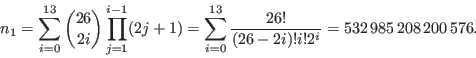
Los rotores podían ser colocados, cada uno, en una de 26 posibles maneras iniciales, por lo que el conjunto de los tres rotores daba $n_3=26^3 = 17\,576$ posiciones iniciales. En cada rotor se colocaba un disco de 26 dientes, por lo que se tenía hasta $n_4=26!$ posibles discos, mas como los discos debían ser distintos, para evitar ataques ``de frecuencias'' a los textos cifrados, se tenía hasta $n_4(n_4-1)(n_4-2)$ posibilidades para configurar los tres rotores.

Finalmente, si se usara una permutación fija, entonces el sistema de cifrado sería susceptible de ser atacado mediante frecuencias: los caracteres que más aparecieran en el texto cifrado corresponderían a los que aparezcan más en el idioma del texto en claro. Para evitar esto, los rotores iban girando, a manera de un tacómetro, al cifrar letra a letra. El giro de los rotores se hacía mediante anillos que descubrían tan solo uno de los caracteres en los rotores. La ingeniería de Enigma hacía que al fijar la disposición de los primeros dos anillos, la del tercero quedaba determinada. Así pues, se tenía $n_5=26^2 = 676$ posibilidades iniciales.

En consecuencia, el número de posibles claves para las máquinas Enigma de tres rotores era

$$n_1\,n_2\,n_3\,n_4(n_4-1)(n_4-2)\,n_5$$

que es un número gigantesco, del orden de $10^{114}$ (se estima, por ejemplo, que el número de átomos en el Universo es ``apenas'' del orden de $10^{80}$).

El Ejército Alemán utilizaba exactamente 6 pares en el tablero de conexiones, con un reflector fijo, y tres discos determinados para los rotores, por lo que el número de claves efectivas era

$$\frac{26!}{(14)!6!2^6}\,n_3\,n_5$$

que es del orden de $7\times 10^{18}$ (siete millones de billones).

Ahora bien, en el alfabeto de 26 caracteres latinos hay

$$\sum_{i=0}^{13}{26\choose 2i}\,{2i\choose i}\,i!$$

involuciones, entre las que estaban las generadas por máquinas Enigma, y este número es del orden de $1\times 10^{18}$ (un millón de billones). Así pues, varias claves darían una misma involución de cifrado y descifrado. Para quebrantar el esquema de Enigma, más que calcular la clave utilizada, era importante caracterizar la involución utilizada.

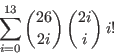
La Criptología en Polonia se desarrollaba en los años 20 y principios de los 30 bajo la conducción del prof. Zdzisaw Krygowski, procedente de Poznan y anteriormente rector de la Politécnica de Lwów, junto con tres ex-alumnos suyos: Marian Rejewski, Henryk Zygalski y Jerzy Rózycki, quienes en los 30 lograron descifrar comunicaciones cifradas con Enigma al poder reconocer las involuciones utilizadas.

Figura 2: Marian Rejewski, Henryk Zygalski y Jerzy Rózycki.

Rejewski hizo dos observaciones importantes: con el álgebra de permutaciones descubrió que toda involución producida por Enigma era el producto de 13 transposiciones (con símbolos ajenos a pares), y, en consecuencia, ninguna letra se cifraba con ella misma, por lo que, por ejemplo, un trigrama jep no podía corresponder a der. Utilizando primeros modelos de Enigma de tipo comercial, Rejewski hizo un estudio algebraico completo de las involuciones de Enigma y tras de ver que los cifrados no correspondían a su análisis hizo un descubrimiento esencial: la permutación del tambor inicial de la Enigma militar había sido cambiada respecto a la versión original comercial. Mediante la conversión de un mero formulismo idiomático, como un ``buenos días'', pudo descubrir la permutación en el tambor de entrada, desde 1932. Años más tarde, en 1939, cuando Rejewski explicó a criptólogos ingleses cuál era la permutación de entrada, Dillwin Knox, fundador de Blenchley Park se enfureció por la simpleza del método, escribió: ``Era una cosa tan obvia de hacerse, incluso algo tonto, que ni Alan Turing ni yo pensábamos que era algo que valiera la pena intentarse''.

En la práctica, en las comunicaciones militares, el elemento principal que variaban las partes comunicantes alemanas era la configuración inicial de los rotores: Tres letras indicaban cuál debía ser la posición inicial. Cuando se enviaba un criptograma, al inicio de él se incluía la configuración inicial. Debido al ruido de las comunicaciones por radio, ese trigrama se repetía y la cadena de 6 caracteres se cifraba a su vez con Enigma. Así, si por ejemplo csg era la configuración inicial, al inicio debía colocarse repetida, csgcsg, y luego debía ser cifrada, digamos jhnqbs. Rejewski sabía que la primera y la cuarta permutaciones cifraban un mismo símbolo, la segunda y la quinta también, al igual que la tercera y la sexta. Así que recolectando varios mensajes, podía descubrir las composiciones de la ``clave del día'', y mediante operaciones algebraicas guiar una búsqueda para descubrirla por completo. De hecho, Rejewski resultó beneficiado de que en septiembre de 1932, Hans-Thilo Schmidt, agente que trabajaba en una oficina de cifrado del Ejército Alemán, contactó al Cap. Gustave Bertrand, del Servico de Inteligencia Francés ofreciéndole materiales que incluían las claves del día utilizadas en dos meses. Bertrand hizo llegar esta información a los polacos, con lo que Rejewski pudo verificar que sus técnicas de quebrantamiento eran correctas. Los criptólogos polacos pudieron incluso mecanizar el procedimiento de Rejewski. Inventaron unos ciclómetros, consistentes de rotores de Enigma, en los que se aplicaba varios preámbulos de seis caracteres y producían la clave del día con el que habían sido producidos los criptogramas correspondientes.

Entre 1934 y 1938 se construyeron en Varsovia, en la fábrica Wytwórnia Radiotechniczna, AVA, 17 máquinas que cifraban según la Enigma militar cuyo diseño partía de un primer modelo de la Enigma comercial de los 20. El constructor de estas réplicas fue el Ing. Antoni Palluth, colaborador cercano de Rejewski, Zygalski y Rózycki. Marian Rejewski diseñó también las primeras bombas: ensambles de máquinas Enigma para probar automáticamente del orden de las $26^3$ posibilidades. Se les nombró ``bombas'', modestamente, debido al ruido que hacían. La primera se fabricó en AVA en noviembre de 1938 e incorporaba 6 réplicas de Enigma. Al mismo tiempo, Zygalski inventó un sistema de ``placas perforadas'' que fueron empleadas en los ciclómetros.

Hasta 1939, el Gobierno Polaco era capaz de descifrar las comunicaciones alemanas de las S.S. y del Ejército de Tierra, pero carecía de capacidad para oponerse al ataque de la blitzkrieg, la guerra motorizada alemana. Además, para entonces las máquinas Enigma alemanas habían sido dotadas de más rotores, lo que hacía inútiles a las réplicas hechas en Polonia, hecho que fue detectado por los polacos desde diciembre de 1938. La construcción de los correspondientes ciclómetros excedía las capacidades industriales y financieras del gobierno de Polonia. La criptología polaca era fromidable en el plano intelectual, pero estaba sujeta a limitaciones materiales. Un recuento personal de estos trabajos lo escribió el propio Rejewski [9].

Del 24 al 27 de julio de 1939, en Syry, entre Varsovia y Lublin, el director del Biuro Szyfrów polaco, Gwido Karol Langer, y otros oficiales, se reunieron con criptólogos franceses e ingleses, Dillwyn Knox participó por la parte inglesa y Gustave Bertrand por la francesa, y les entregaron réplicas polacas de la máquina Enigma militar así como los procedimientos para quebrantar el esquema. Esta fue una decisión del Estado Mayor Polaco ante la inminencia de la guerra, decisión que fue muy afortunada pues los alemanes tenían una gran confianza en la inviolabilidad de Enigma y no pudieron confirmar en su momento que sus comunicaciones eran interceptadas.

"Inglaterra: ¡Esto ha sido obra tuya!"
Cartel de propaganda nazi donde se trata de inculpar a Inglaterra por el ataque alemán de septiembre de 1939

El 5 de septiembre de 1939, cuatro días después del inicio de la invasión alemana a Polonia, los criptólogos polacos recibieron la orden de abandonar el país. Fueron llevados a Francia a través de Rumanía e Italia, y a partir de octubre de 1939 se establecieron en el castillo de Vignolles, cerca de Gretz-Armaivilliers, en Seine-et-Marne, a unos cuarenta kilómetros al este de París, y continuaron con su labor de quebrantamiento de comunicaciones alemanas, ahí, cooperando con antiguos combatientes españoles republicanos. En enero de 1940, el Gobierno Inglés solicita que los criptólogos polacos sean llevados a Bletchley Park, pero el Gobierno Francés se opone, sin embargo acepta que Alan Turing visite Vignolles. El 17 de enero, los polacos logran recuperar las primeras claves del día de la Enigma de cuatro rotores. En mayo de 1940, los alemanes cambian los procedimientos de transmisión de las claves del día y se invade Francia. El 21 de mayo, Turing en Bletchley Park logra recuperar las nuevas claves del día y quebrantar las comunicaciones entre la Luftwaffe y el Ejército de Tierra. En junio de 1940, con el territorio francés dividido, el Gobierno de Vichy desmantela al Ejército Francés, y el Gobierno Polaco en el Exilio facilita que los criptólogos polacos sean transportados a Argelia, pues las actividades de la Inteligencia Francesa, de acuerdo con el Armisticio pactado por Pétain, quedaron suspendidas. Sin embargo, en octubre de 1940 fueron llevados de nuevo a Francia, a Uzés, al castillo de Fouzes.

Ahí estuvieron en una situación ambigua: por un lado para el Gobierno de Vichy habían de supervisar las comunicaciones alemanas para verificar que las condiciones del Armisticio se cumplieran, pero por otro lado transmitían al Gobierno Polaco en el Exilio y a Bletchley Park las comunicaciones alemanas interceptadas, entre las que estaban las comunicaciones de la Gestapo en el Territorio Libre de Francia. Al ver que mandos alemanes utilizaban todavía los esquemas previos de cifrado con Enigma, comprobaron que ellos desconocían que los esquemas habían sido quebrantados. Parte del grupo de criptólogos polacos se mantuvo en Argel, entre ellos Rózycki, para interceptar las comunicaciones del Ejército Alemán en el Norte de Africa. El 9 de enero de 1942, mueren en un naufragio Ciezki, Gralinski y Smolinski, oficiales del Biuro Szyfrów, y el criptólogo Rózycki, cuando se transportaban hacia Francia. En septiembre de 1942, los alemanes detectan al grupo de criptología en Fouzes, y el Gobierno de Vichy, de manera paradójica, facilita que los alemanes acudan en noviembre a desmantelar el centro que Vichy mismo había establecido. Prevenidos por Bletchley Park, se ordena evacuar de manera urgente al grupo polaco. Sin embargo, se da prioridad en la evacuación a los oficiales franceses y se deja a los polacos a su suerte. Algunos lograron llegar a España, tras pagar a guías estafadores, y fueron luego llevados a Inglaterra por la Cruz Roja. Rejewski y Zygalski llegaron a España pero fueron detenidos por la Guardia Civil franquista en Lérida. Mediante la intervención de la Embajada Británica en Madrid, fueron liberados y transportados también a Inglaterra. Otros, como Antoni Palluth, constructor de la réplicas polacas de Enigma, y Gwido Karol Langer, director del Biuro Szyfrów, fueron aprehendidos por los alemanes en la frontera con España. A pesar de torturas infringidas por la Gestapo, no develaron la naturaleza de sus actividades, por lo que el secreto del quebrantamiento de Enigma se mantuvo. Palluth murió en el bombardeo del 10 de abril de 1944 al campo de concentración en Sachsen Hausen-Oranienburg, donde era prisionero. Otros oficiales polacos fueron liberados de ese campo en mayo de 1945 por tropas yanquis. Sobre ellos pesó la sospecha de que el fracaso de su evacuación se había debido a una filtración por ellos mismos, lo que era absurdo pues el secreto de Enigma se mantuvo. Luego de la Liberación, oficiales como el propio Langer, exigieron a las autoridades francesas una aclaración sobre este punto, pero nunca la obtuvieron. Gente que había hecho una gran contribución al triunfo aliado veía así manchado su honor. En Inglaterra, Rejewski y Zygalski trabajaron para el Gobierno Polaco en el Exilio. Zygalski se estableció ahí, enseñando en la Universidad de Surrey en Londres. Murió en 1978. Rejewski regresó a Polonia en noviembre de 1946, en la República Popular no le fue posible emplearse como matemático en centros de educación superior (la gente ligada con el Gobierno en el Exilio le era poco confiable al régimen) y no quiso involucrarse en la seguridad del estado, así que trabajó como un modestísimo administrador de empresas estatales en Bydgoszcz, jubilándose en febrero de 1967. Murió en 1980.

En los 40, los criptólogos ingleses en Bletchley Park, entre ellos Alan Turing de manera relevante, se abocaron a descifrar, con éxito, las comunicaciones de la Marina Alemana, partiendo de la metodología polaca. En 1974 David Kahn escribió un artículo para The New York Times mostrando la contribución de los polacos en la criptología de los Aliados en la Segunda Guerra Mundial. En 1999, cuando Polonia se incorporó a la OTAN, se reconoció formalmente este trabajo y en 2004 se colocó una placa en el museo de Bletchley Park acreditando a Rejewski, Zygalski y Rózycki los primeros quebrantamientos de Enigma.

Placa conmemorativa, en Bletchley Park, dedicada a los criptólogos polacos

Figura 3: Timbre postal polaco: ``Polacos en el mundo''.