


Siguiente: Método de llave pública
Un nivel arriba: En campos finitos
Anterior: Algoritmo de Silver (1978)
Sea
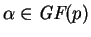 un generador. Sea F un conjunto de primos en
un generador. Sea F un conjunto de primos en
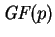 .
.
- 1.
- Supongamos que
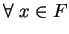 se ha calculado
se ha calculado
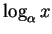 .
Dado
.
Dado
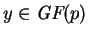 ,
elegimos
,
elegimos
![$Z\in [\![0,p-2]\!]$](img196.gif) aleatoriamente y calculamos
aleatoriamente y calculamos
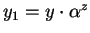 .
Si y1 se factoriza completamente con factores en F, es decir, si
expresamos
.
Si y1 se factoriza completamente con factores en F, es decir, si
expresamos
entonces
Así pues, expresamos a
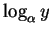 en términos de los
números
en términos de los
números
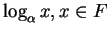 .
Veamos pues cómo calcular
a estos últimos.
.
Veamos pues cómo calcular
a estos últimos.
- 2.
- Cálculo de
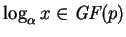 .
Generemos card(F) exponentes
.
Generemos card(F) exponentes
![$z\in [\![0, p-2]\!]$](img203.gif) tales que
tales que 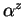 se
factoriza completamente en F:
se
factoriza completamente en F:
Entonces
lo cual dará un sistema (no singular) de card(F) ecuaciones
lineales en
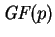 ,
con card(F) incógnitas
,
con card(F) incógnitas
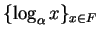 .
La dificultad de esta etapa consiste en elegir a los números z.
Otro problema es la elección del mismo conjunto F. Un criterio es
el siguiente:
.
La dificultad de esta etapa consiste en elegir a los números z.
Otro problema es la elección del mismo conjunto F. Un criterio es
el siguiente:
- 3.
- Sea
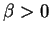 y sea
y sea
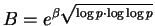 .
Elijamos
.
Elijamos
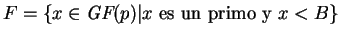 .
.
El algoritmo descrito tendrá
complejidad en tiempo
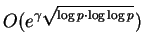 donde
donde 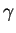 es una constante.
es una constante.
Guillermo Morales-Luna
2000-10-29
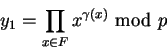
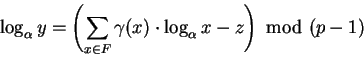
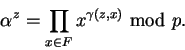
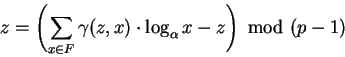
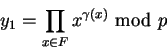
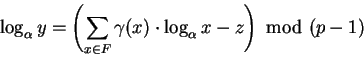
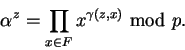
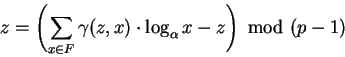
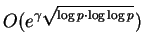 donde
donde