


Siguiente: Diversos esquemas de autentificación
Un nivel arriba: Firmas digitales
Anterior: Firmas digitales
Supongamos un esquema de llave pública. En grupo de usuarios 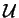 cada uno U posee una pareja (eU,dU) formada por sus llaves pública y secreta, respectivamente. Cualquier mensaje m hacia U se encripta como
c=F(m,eU) y U lo desencripta como
m=G(c,dU).
En un tal esquema, se considera el esquema de firmado
cada uno U posee una pareja (eU,dU) formada por sus llaves pública y secreta, respectivamente. Cualquier mensaje m hacia U se encripta como
c=F(m,eU) y U lo desencripta como
m=G(c,dU).
En un tal esquema, se considera el esquema de firmado
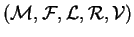 ,
donde
,
donde
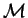 es el conjunto de mensajes,
es el conjunto de mensajes,
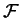 coincide con
coincide con 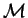 (que a su vez coincide con el de cifrados),
(que a su vez coincide con el de cifrados),
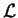 coincide con
coincide con 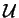 ,
,
-
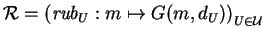 ,
y
,
y
-
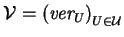 donde
donde
![$\forall U\in{\cal U}:\ \begin{array}[t]{rcl}
\mbox{\it ver}_U(m,f)=\mbox{\it S...
...ox{\it ver}_U(m,f)=\mbox{\it No} &\Leftrightarrow& m\not=F(f,e_U)
\end{array}$](img297.gif)
Si además de firmar se ha de encriptar, se puede proceder como sigue:
Firmar y luego encriptar
- 1.
- Dado el mensaje m el remitente calcula la firma correspondiente,
f= G(m,dR).
- 2.
- Encripta la pareja (m,f) usando la llave pública del destinatario:
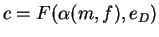 ,
donde
,
donde
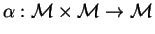 es una función de apareamiento.
es una función de apareamiento.
- 3.
- El destinatario, recibe c y lo desencripta con su llave secreta:
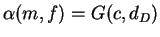 .
.
- 4.
- El destinatario verifica la firma:
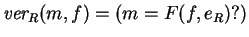 .
.
¡El orden es importante! El procedimiento siguiente es inseguro.
Encriptar y luego firmar
- 1.
- Dado el mensaje m el remitente lo encripta usando la llave pública del destinatario:
c=F(m,eD).
- 2.
- Calcula la firma correspondiente al mensaje cifrado,
f= G(c,dR).
- 3.
- El destinatario, recibe la pareja (c,f). Verifica la firma:
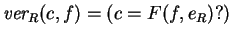 .
.
- 4.
- El destinatario queda convencido que el remitente es R.
- 5.
- El destinatario desencripta con su llave secreta:
m=G(c,dD).
En efecto, si un intruso S recibe la pareja (c,f), entonces
- 1.
- calcula su propia firma correspondiente al mensaje cifrado:
f'= G(c,dS).
- 2.
- El destinatario, recibe la pareja (c,f'). Verifica la firma, usando la llave de S:
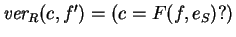 .
.
- 3.
- El destinatario queda convencido que el remitente es S.
- 4.
- El destinatario desencripta con su llave secreta:
m=G(c,dD).
S pues ha suplantado a R.



Siguiente: Diversos esquemas de autentificación
Un nivel arriba: Firmas digitales
Anterior: Firmas digitales
Guillermo Morales-Luna
2000-10-29
![$\forall U\in{\cal U}:\ \begin{array}[t]{rcl}
\mbox{\it ver}_U(m,f)=\mbox{\it S...
...ox{\it ver}_U(m,f)=\mbox{\it No} &\Leftrightarrow& m\not=F(f,e_U)
\end{array}$](img297.gif)
![$\forall U\in{\cal U}:\ \begin{array}[t]{rcl}
\mbox{\it ver}_U(m,f)=\mbox{\it S...
...ox{\it ver}_U(m,f)=\mbox{\it No} &\Leftrightarrow& m\not=F(f,e_U)
\end{array}$](img297.gif)