


Siguiente: Encriptamiento por bloques
Un nivel arriba: Introducción a criptografía y
Anterior: Algo que no es
Un buen sistema criptográfico ha de tener varias características:
- pequeñas variaciones de textos llanos: grandes variaciones de textos cifrados,
- los tamaños de los textos planos deben ser comparables con los cifrados,
- los textos cifrados deben calcularse eficientemente a partir de los planos, y
- la relación entre textos planos y cifrados debe ser impredecible.
Un mal sistema criptográfico se caracteriza porque:
- aparenta una relación aleatoria entre planos y cifrados, pero en realidad no lo es,
- es susceptible a criptoanálisis elementales,
- el cálculo de cifrados es ineficiente en tiempo y en espacio, y
- es vulnerable a sus propios fabricantes.
Un sistema criptográfico típico de llave secreta consta de los objetos siguientes
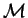 :
un espacio de mensajes,
:
un espacio de mensajes,
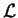 :
un espacio de llaves,
:
un espacio de llaves,
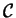 :
un espacio de cifrados de textos,
:
un espacio de cifrados de textos,
-
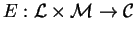 :
función de encriptamiento,
:
función de encriptamiento,
-
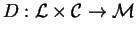 :
función de desencriptamiento, tales que
:
función de desencriptamiento, tales que
-
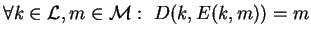 &
&
-
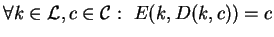 .
.
El sistema es seguro si a pesar de conocer E(k,m),
desconociendo k no se puede calcular m.
Ejemplo. Rellenado de una sola vez (one-time pad) En
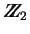 la operación suma
la operación suma 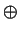 , u ``O''-excluyente, es de orden 2:
, u ``O''-excluyente, es de orden 2:
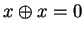 , y
, y 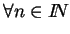 , la misma operación componente a componente
cumple lo mismo:
, la misma operación componente a componente
cumple lo mismo:
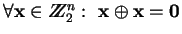 .
Así pues, se puede tomar
.
Así pues, se puede tomar
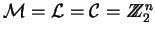 y
y
el sistema es seguro pues conocido
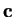 si no se conoce
si no se conoce
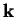 no es recuperable
no es recuperable
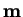 (de hecho, es posible generar cualquier
(de hecho, es posible generar cualquier
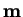 pues siempre existe
pues siempre existe
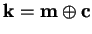 tal que
tal que
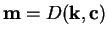 .
.
Ejemplo. Transformaciones lineales no-singulares
Sea
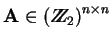 una matriz tal que
una matriz tal que
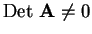 y sea
y sea
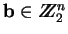 .
Entonces la pareja
.
Entonces la pareja
 ,
que contiene n2+n ``entradas'' en
,
que contiene n2+n ``entradas'' en
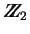 ,
determina una transformación afín
,
determina una transformación afín
con inversa
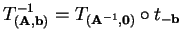 ,
donde
,
donde 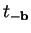 es la translación
es la translación
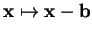 .
.
Ejemplo. Permutaciones-sustituciones de Shannon
Sustituciones. Para 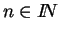 , sea
, sea 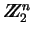 el espacio de cadenas binarias de longitud n. Sea
el espacio de cadenas binarias de longitud n. Sea
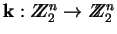 una permutación.
A cada mensaje
una permutación.
A cada mensaje
![$\mbox{\bf m}=\left[m_i\right]_{i\leq l}\in\left(Z\!\!\!Z_2^n\right)^*$](img35.gif) se le asocia el código
se le asocia el código
![$\mbox{\bf c}=\left[\mbox{\bf k}(m_i)\right]_{i\leq l}\in\left(Z\!\!\!Z_2^n\right)^*$](img36.gif) .
En este caso se tiene un espacio de llaves de tamaño
.
En este caso se tiene un espacio de llaves de tamaño
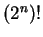 .
.
Permutaciones. Sea
![$\mbox{\bf k}:[\![1,n]\!] \rightarrow [\![1,n]\!]$](img38.gif) una permutación.
A cada mensaje, dividido en bloques,
una permutación.
A cada mensaje, dividido en bloques,
![$\mbox{\bf m}=\left[m_i=\left[a_{ij}\right]_{j\leq n}\right]_{i\leq l}\in\left(Z\!\!\!Z_2^n\right)^*$](img39.gif) se le asocia el código
se le asocia el código
![$\mbox{\bf c}=\left[\left[a_{i\mbox{\scriptsize\bf k}(j)}\right]_{j\leq n}\right]_{i\leq l}\in\left(Z\!\!\!Z_2^n\right)^*$](img40.gif) .
En este caso se tiene un espacio de llaves de tamaño n!.
.
En este caso se tiene un espacio de llaves de tamaño n!.



Siguiente: Encriptamiento por bloques
Un nivel arriba: Introducción a criptografía y
Anterior: Algo que no es
Guillermo Morales-Luna
2000-10-29
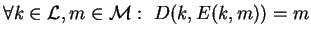 &
&
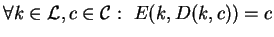 .
.
![]() la operación suma
la operación suma ![]() , u ``O''-excluyente, es de orden 2:
, u ``O''-excluyente, es de orden 2:
![]() , y
, y ![]() , la misma operación componente a componente
cumple lo mismo:
, la misma operación componente a componente
cumple lo mismo:
![]() .
Así pues, se puede tomar
.
Así pues, se puede tomar
![]() y
y 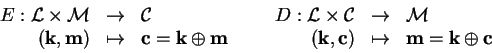
![]() ,
donde
,
donde ![]() es la translación
es la translación
![]() .
. ![]() , sea
, sea ![]() el espacio de cadenas binarias de longitud n. Sea
el espacio de cadenas binarias de longitud n. Sea
![]() una permutación.
A cada mensaje
una permutación.
A cada mensaje
![]() se le asocia el código
se le asocia el código
![]() .
En este caso se tiene un espacio de llaves de tamaño
.
En este caso se tiene un espacio de llaves de tamaño
![]() .
. ![]() una permutación.
A cada mensaje, dividido en bloques,
una permutación.
A cada mensaje, dividido en bloques,
![]() se le asocia el código
se le asocia el código
![$\mbox{\bf c}=\left[\left[a_{i\mbox{\scriptsize\bf k}(j)}\right]_{j\leq n}\right]_{i\leq l}\in\left(Z\!\!\!Z_2^n\right)^*$](img40.gif) .
En este caso se tiene un espacio de llaves de tamaño n!.
.
En este caso se tiene un espacio de llaves de tamaño n!.