


Siguiente: Triple DES
Un nivel arriba: Data Encryption Standard (DES)
Anterior: Data Encryption Standard (DES)
El estándar de encriptamiento de datos, Data Encryption Standard (DES), ha sido de los más utilizados en la historia de la criptografía:
- Se desarrolló en los años 70, por IBM, principalmente.
- En 1977 se adoptó como un estándar por la Oficina Nacional de Estándares (NBS: National Bureau of Standards, en la actualidad el National Institute of Standards and Technology) del Gobierno de los EUA.
- Es de encriptamiento por bloques, con bloques de 64 bits.
- Utiliza llaves de 56 bits (dadas en 8 bytes, en cada uno de los cuales 7 bits son de la llave y el octavo es de paridad).
- Consecuentemente, el espacio de búsqueda para la llave es de tamaño 256 (en promedio se requiere de 255 pasos de búsqueda).
- El encriptamiento se hace con 16 ciclos de reiteración. En cada ciclo, los paraámetros de la función de encriptamiento dependen de los bloques de datos y de llaves, actuales y previos.
- En cada ciclo, la (sub-)llave
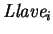 ,
,
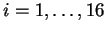 se construye mediante un algoritmo de preparación de llaves (key scheduling algorithm).
se construye mediante un algoritmo de preparación de llaves (key scheduling algorithm).
Dado un mensaje
 de 64 bits, es decir, 8 bytes,
de 64 bits, es decir, 8 bytes,
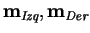 de 4 bytes cada uno, se procede como sigue:
de 4 bytes cada uno, se procede como sigue:
- 1.
- Sea
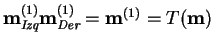 ,
donde T es una permutación.
,
donde T es una permutación.
- 2.
- Para
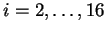 hágase
hágase
donde
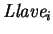 tiene una longitud de 48 bits.
tiene una longitud de 48 bits.
- 3.
-
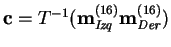 .
.
El cálculo de
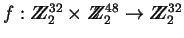 ,
,
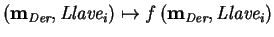 utiliza 8 transformaciones
utiliza 8 transformaciones
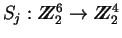 ,
,
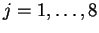 ,
llamadas S-cajas, fijadas de antemano por los estándares.
f se calcula como sigue:
,
llamadas S-cajas, fijadas de antemano por los estándares.
f se calcula como sigue:
- 1.
- Duplicando bits en 16 posiciones, la cadena
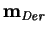 de 32 bits se expande a una cadena
de 32 bits se expande a una cadena
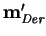 de 48 bits.
de 48 bits.
- 2.
- Sea
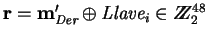 .
.
- 3.
- Escríbase
![$\mbox{\bf r}=\left[\mbox{\bf r}_j\right]_{j=1}^8$](img71.gif) ,
donde cada
,
donde cada
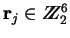 es una cadena de 6 bits.
es una cadena de 6 bits.
- 4.
- Hágase
![$f\left(\mbox{\bf m}_{\mbox{\scriptsize\it Der}}^{(i-1)},\mbox{\it Llave}_i\righ...
...\right)\right]_{j=1}^4 P\left[S_{j}\left(\mbox{\bf r}_{j}\right)\right]_{j=5}^8$](img73.gif) ,
donde P es una permutación
,
donde P es una permutación
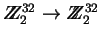 .
.
En cuanto a la generación de sub-llaves, dada la llave del usuario de 56 bits, primero se transpone a sus bits, y se fracciona en dos partes de 28 bits cada una. Se va rotando a estas partes uno o dos bits a la izquierda, dependiendo del índice del ciclo, y de acuerdo con una regla fija, se compone a las partes para producir la llave
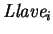 de 48 bits:
de 48 bits:
- 1.
- Sea
![$\mbox{\it Llave}=\left[k_i\right]_{i=1}^{64}$](img75.gif) una llave dada por 64 bits. Los bits k8i,
una llave dada por 64 bits. Los bits k8i,
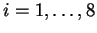 son de paridad. Se les descarta y los restantes forman la llave de 56 bits propia del usuario.
son de paridad. Se les descarta y los restantes forman la llave de 56 bits propia del usuario.
- 2.
- Sea
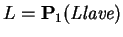 la cadena de 56 bits formada mediante la aplicación de una permutación
la cadena de 56 bits formada mediante la aplicación de una permutación
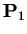 ,
a
,
a
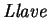 .
Escríbasela como un par de cadenas de 28 bits,
[C0,D0]=L.
.
Escríbasela como un par de cadenas de 28 bits,
[C0,D0]=L.
- 3.
- Para cada ciclo
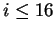 ,
hágase
,
hágase
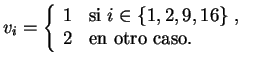
En otras palabras, de acuerdo con el índice de cada ciclo se ha de rotar como se indica a continuación:
| Ciclo i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
| Rotaciones vi |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
Sea
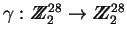 la rotación consistente de ``correr un lugar hacia la izquierda''.
la rotación consistente de ``correr un lugar hacia la izquierda''.
- 4.
- Para cada
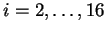 hágase
hágase
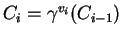 ,
,
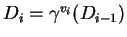 y sea
y sea
![$\mbox{\it Llave}_i=\mbox{\bf P}_2([C_i,D_i])$](img85.gif) la llave de 48 bits formada mediante una permutación
la llave de 48 bits formada mediante una permutación
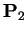 .
.
Para desencriptar se sigue el mismo procedimiento, pero en sentido inverso de aplicación.
Observaciones:
- Las S-cajas definen transformaciones que no son lineales ni afines. En tanto sean más complejas, la seguridad será mayor.
- Una llave es débil si
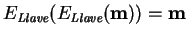 .
.
- Propiedad de complemento. Si
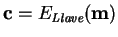 entonces
entonces
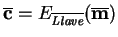 .
.
- En la actualidad, la llave resulta pequeña.
- La implementación en hardware de las S-cajas es propiedad de IBM y no se ha publicado su diseño, el cual puede ser un elemento de vulnerabilidad.
Un posible ataque:
- 1.
- Escójase
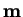 .
.
- 2.
- Obténgase los cifrados
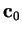 de
de
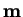 y
y
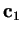 de
de
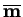 ,
así
,
así
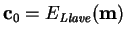 y
y
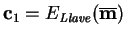 .
.
- 3.
- Para las 255 llaves
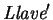 cuyo bit más significativo es 0, revísese si
cuyo bit más significativo es 0, revísese si
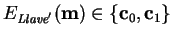 .
En tal caso, se tendrá evidencia de que
.
En tal caso, se tendrá evidencia de que
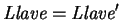 si
si
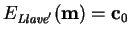 o bien de que
o bien de que
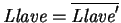 si
si
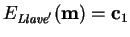 .
.



Siguiente: Triple DES
Un nivel arriba: Data Encryption Standard (DES)
Anterior: Data Encryption Standard (DES)
Guillermo Morales-Luna
2000-10-29
![]() de 64 bits, es decir, 8 bytes,
de 64 bits, es decir, 8 bytes,
![]() de 4 bytes cada uno, se procede como sigue:
de 4 bytes cada uno, se procede como sigue:
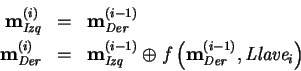
![]() ,
,
![]() utiliza 8 transformaciones
utiliza 8 transformaciones
![]() ,
,
![]() ,
llamadas S-cajas, fijadas de antemano por los estándares.
f se calcula como sigue:
,
llamadas S-cajas, fijadas de antemano por los estándares.
f se calcula como sigue:
![]() de 48 bits:
de 48 bits:
