Definición 1.2
Los siguientes tipos de proposiciones son muy importantes:
- TAUTOLOG´iA.
- Proposición verdadera bajo toda asignación.
- CONTRADICCIÓN.
- Proposición cuya negación es
tautología.
Distinguimos también las nociones siguientes:
Decimos que
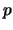
es
EQUIVALENTE a
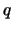
, y escribimos
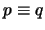
, si
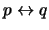
es tautología.