Posterior: Optimización de formas conjuntivas Arriba: Semántica Anterior: Cálculo de consecuencias lógicas

Formalización de problemas de lógica

Presentaremos algunos ejemplos de formalización de acertijos lógicos.

Ejemplo 1.4   La caja de seguridad de una empresa posee 5 cerrojos cuyas llaves $\ell_1,\ell_2,\ell_3,\ell_4,\ell_5$ están custodiadas por 5 ejecutivos $e_1,e_2,e_3,e_4,e_5$. Cada ejecutivo posee dos llaves:

$e_1$ posee las llaves $\ell_1$ y $\ell_3$,

$e_2$ posee las llaves $\ell_1$ y $\ell_4$,

$e_3$ posee las llaves $\ell_2$ y $\ell_4$,

$e_4$ posee las llaves $\ell_3$ y $\ell_5$ y

$e_5$ posee las llaves $\ell_1$ y $\ell_5$.

Para abrir la caja de seguridad se necesita abrir los 5 cerrojos. ¿Cuál es el mínimo número de ejecutivos que deben estar presentes para abrir la caja?

Explicación. Resumamos el planteamiento con una matriz $5\times 5$, $M=\left(m_{ij}\right)_{i\leq 5}^{j\leq 5}\in \mbox{\rm Dos}^{5\times 5}$ haciendo $m_{ij}=1$ si y sólo si el $i$-ésimo ejecutivo posee a la $j$-ésima llave,

$$M=\left(\begin{array}{ccccc} 1 & 0 & 1 & 0 & 0 \\ 1 & 0 &... ... 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 0 & 1 %%\\ \end{array}\right)$$

Simbolicemos:

$e_i$:

El ejecutivo $e_i$ está presente.

$f_j$:

Se cuenta con la llave $\ell_j$.

Evidentemente, se tiene las equivalencias:

$$\begin{eqnarray*} f_1 &\equiv& e_1 \lor e_2 \lor e_5 \\ f_2 &\equiv& e_3 \\ ... ...4 \\ f_4 &\equiv& e_2 \lor e_3 \\ f_5 &\equiv& e_4 \lor e_5 \end{eqnarray*}$$

La condición para que se abra la caja es entonces

$$\begin{eqnarray*} \mbox{\it AbrirCaja} &\equiv& f_1 \land f_2 \land f_3 \land f... ...d \left[e_2 \lor e_3\right] \land \left[e_4 \lor e_5\right] \end{eqnarray*}$$

y al desarrollar por distibutividad el último miembro se obtiene

$$\begin{eqnarray*} \mbox{\it AbrirCaja} &\equiv& \left[e_1 \land e_3 \land e_... ... & & \left[e_1 \land e_2 \land e_3 \land e_4 \land e_5\right] \end{eqnarray*}$$

y utilizando las propiedades de absorción se tiene

$$\begin{eqnarray*} \mbox{\it AbrirCaja} &\equiv& \left[e_1 \land e_3 \land e_... ...e_4\right] \lor \\ & & \left[e_3 \land e_4 \land e_5\right] \end{eqnarray*}$$

de donde se ve que hay 4 posibilidades de que con 3 ejecutivos se abra la caja de seguridad. De la primera expresión dada para abrir la caja, al utilizar las leyes de De Morgan generalizadas, obtenemos que, para no abrir la caja:

$$\overline{\mbox{\it AbrirCaja}} \equiv \left[\neg e_1 \land... ...and \neg e_3\right] \lor \left[\neg e_4 \land \neg e_5\right]$$

$\quad\Box$

Ejemplo 1.5   Se ha cometido un robo cuantioso a un cierto establecimiento. Los criminales huyeron en auto. Luego se captura a tres peligrosos sujetos: Alberto, Benito y Carlos. Se tiene los hechos siguientes:

• Nadie más que Alberto, Benito y Carlos pudo participar en el asalto.
• Carlos no puede participar en fechoría alguna si no es en la compañía de Alberto.
• Benito no sabe manejar.

¿Es acaso Alberto culpable de participar en el asalto?

Explicación. Simbolicemos:

$A$:

Alberto participó en el asalto.

$B$:

Benito participó en el asalto.

$C$:

Carlos participó en el asalto.

Las tres condiciones son entonces equivalentes a las siguientes:

• $H_1:=A\lor B\lor C$.
• $H_2:=C\rightarrow A$.
• $H_3:=B\rightarrow (A\lor C)$.

Las dos primeras fórmulas son evidentes. La tercera se debe a que si hubiese participado $B$ entonces él no pudo ir manejando. Así que debió participar uno más. Se ha de decidir si acaso $\{H_1,H_2,H_3\}\models A$. Denotemos a la conjunción de las hipótesis como $P:=H_1\land H_2\land H_3$. Ya que se tiene la equivalencia $p\rightarrow q\equiv \neg p \lor q$ resulta

$$P\equiv [A\lor B\lor C] \land [\neg C \lor] \land [\neg B \lor A\lor C].$$

Al desarrollar por distributividad, se tiene

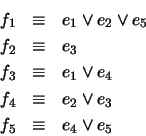
$$\begin{eqnarray*} P &=& \left[A\right] \lor \\ & & \left[A \land B\right] ... ... \neg C\right] \lor \left[C \land \neg B \land \neg C\right] \end{eqnarray*}$$

ahora como $p\land \neg p$ siempre es falso, cualquiera que sea $p$,

$$\begin{eqnarray*} P &=& \left[A\right] \lor \\ & & \left[A \land B\right] ... ...\neg B\right] \lor \left[A \land \neg B \land \neg C\right] \end{eqnarray*}$$

y por las leyes de absorción, $P=A$. Así pues $A$ es culpable. $\quad\Box$
Posterior: Optimización de formas conjuntivas Arriba: Semántica Anterior: Cálculo de consecuencias lógicas