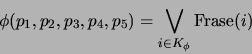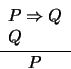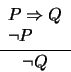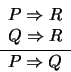


Posterior: Sintaxis
Arriba: Cálculo proposicional
Anterior: Algoritmo de Quine-McCluskey
1. Encuentre a una proposición, que sólo involucre a tres variables proposicionales, que sea equivalente a su propia proposición dual.
2. Muestre que el conjunto de conectivos
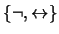 no es completo.
no es completo.
3. A. Pruebe que para cualesquiera
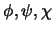 , la proposición
, la proposición 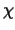 es una consecuencia lógica de
es una consecuencia lógica de  y
y
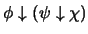 , donde ``
, donde ``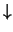 '' es el conectivo NOR:
'' es el conectivo NOR:
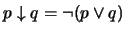 .
.
B. Enuncie y pruebe un resultado similar, considerendo el conectivo NAND:
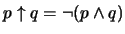 .
.
C. Muestre que cada uno de las mónadas de conectivos
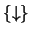 y
y 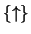 constituyen en sí sendos conjuntos completos de conectivos.
constituyen en sí sendos conjuntos completos de conectivos.
4. Exprese como una conjunción de cláusulas, de manera mínima, a las siguientes proposiciones:
-
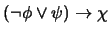
-
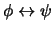
-
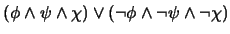
-
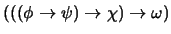
5. Minimice a la proposición
donde
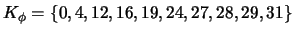 .
.
6. En buenos tiempos idos, al Comité Organizador de algunos Juegos, los paises ISR, ARB, EUA, RDA y URS le establecieron como una condición para su asistencia que se garantizara una coyuntura favorable.
Específicamente, tal coyuntura significaba que se cumplieran simultáneamente las proposiciones siguientes:
- Alguno de ISR o ARB, o ambos, debería asistir.
- Alguno de EUA o URS, pero no ambos, debería estar presente.
- Bien ISR y EUA estarían presentes, o bien ambos faltarían.
- Si RDA asistiera, también la URS debería asistir.
- Si ARB asistiera, entonces bien ISR o bien RDA debeia asistir.
Determine un subconjunto maximal de estos paises que puedieran estar presentes en los Juegos bajo una coyuntura favorable.
7. Una compañía aseguradora establece como condiciones para extender un seguro de vida que el cliente caiga en una de las siguientes categorías:
- Mujeres casadas mayores de 25 años.
- Mujeres solteras menores de 25 años.
- Hombres casados menores de 25 años que no hayan sufrido un accidente automovilístico.
- Hombres casados que no hayan sufrido un accidente automovilístico.
- Hombres casados mayores de 25 años que no hayan sufrido un accidente automovilístico.
Sean
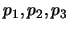 y
y 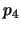 las siguientes proposiciones:
las siguientes proposiciones:
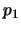 :
:- El cliente ha sufrido algún accidente automovilístico.
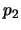 :
:- El cliente es casado.
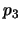 :
:- El cliente es un hombre.
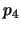 :
:- El cliente es menor de 25 años.
-
Encuentre una proposición mínima, en términos de 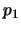 ,
, 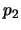 ,
, 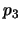 y
y 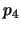 equivalente a las condiciones requeridas para otorgar un seguro.
equivalente a las condiciones requeridas para otorgar un seguro.
8. Reconozca en los siguientes discursos a las proposiciones básicas y exprese a cada uno como una proposición. Revise si la proposición resultante es una tautología, si es consistente o si es una contradicción:
- ``Si los militantes del PRD que provenienen de las antiguas juventudes comunistas del PCM recurren a la Corte para juzgar a la Guerra Sucia entonces renuncian a sus viejas convicciones pero si dejan de recurrir entonces favorecen la impunidad. Ahora bien ocurre una de dos: o bien recurren a la Corte o bien dejan de recurrir. Luego habrán de renunciar a sus viejas convicciones o de favorecer la impunidad''.
- ``Si dos gases tienen la misma temperatura entonces sus moléculas tienen el mismo promedio de energía cinética. Volúmenes iguales de dos gases tienen el mismo número de moléculas. Las
presiones de dos gases son iguales si es el mismo su número de moléculas y además sus energías cinéticas son iguales. Por tanto, dos gases que tienen la misma temperatura y el mismo volumen tienen la misma presión''.
9. Reconozca en los siguientes discursos a las proposiciones básicas y exprese a cada uno como una proposición. Revise si la proposición resultante es una tautología, si es consistente o si es una contradicción:
- ``Todo número entero es primo o es compuesto. Si es compuesto es
un producto de factores primos y en este caso es dividible por los
factores. Un número que no es compuesto es divisible por sí mismo,
luego es divisible por un número primo. Asíque todo número es
divisible por números primos''.
- ``
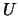 es un subespacio de
es un subespacio de 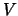 si y sólo si ocurren las siguientes tres condiciones:
si y sólo si ocurren las siguientes tres condiciones: 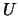 es un subconjunto de
es un subconjunto de 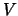 ,
, 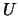 contiene al subespacio cero y
contiene al subespacio cero y 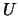 es cerrado. Se sabe que
es cerrado. Se sabe que 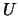 es un
subconjunto de
es un
subconjunto de 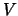 y que si
y que si 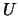 es cerrado entonces
es cerrado entonces 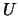 contiene al subespacio cero. Por tanto, si
contiene al subespacio cero. Por tanto, si 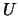 fuera cerrado entonces
fuera cerrado entonces 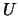 sería un subespacio de
sería un subespacio de 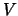 .''
.''
10. Reconozca en los siguientes discursos a las proposiciones básicas y exprese a cada uno como una proposición. Revise si la proposición resultante es una tautología, si es consistente o si es una contradicción:
- ``Si se construyeran albergues antiatómicos, algunos paises se sentirán amenazados y nuestra población tendrá una falsa sensación de seguridad. Si algunos otros paises se sintieran amenazados, podrían iniciar una guerra de advertencia. Por otro lado, si nuestra población tuviera una falsa sensación de paz entonces descuidaría su vigilancia por la paz. Pero además, si no se construyeran los albergues, sufriríamos enormes bajas civiles en el caso de una guerra. Por lo tanto, tenemos la siguiente alternativa: Algunos otros paises iniciarán una guerra de advertencia o sufriremos enormes bajas civiles en el caso de una guerra.''
- ``Una de dos: O el amor se ciego y la felicidad se puede lograr o bien el amor es ciego pero las mujeres son más sensibles que los hombres. El amor no sería ciego si acaso la felicidad se pudiera alcanzar. También las mujeres son más sensibles que los hombres.''
11. Maniqueterra es un país cuyos habitantes se dividen en dos clases: Los que siempre dicen la verdad y los que nunca la dicen. Un turista se dirige a la capital Silia y en un momento se encuentra en una encrucijada: El camino se divide en dos, uno que conduce a Silia y otro que lleva a otra ciudad vecina, Noelia. En el entronque no hay señalamiento alguno, pero al momento de pasar, el turista se encuentra con un maniqueterráneo. ¿Qué pregunta le debe formular el turista, para que de una respuesta ``sí'', entre
las dos únicas posibles ``sí'' o ``no'', el turista deduzca que el camino a la izquierda es el que lleva a Silia?
12. Triclasia es un pais de buenos, de malos y de feos. Los buenos siempre dicen la verdad, los malos nunca la dicen y los feos a veces la dicen y a veces no. Igual que antes, un turista se encuentra con un camino que se bifurca, una ramificación lleva hacia la ciudad que el turista quiere visitar y la otra va hacia
otra. Aquí tampoco hay señalamientos, pero hay tres individuos: Uno bueno, uno malo y uno feo. Por sus solas apariencias, el turista no puede reconocer cuál es cuál.
Construya dos preguntas que el turista deba formular a dos de los individuos presentes, una a cada uno, para que de las respuestas ``sí'' o ``no'' que reciba, deduzca que el de la izquierda es el camino que debe seguir.
13. En el diálogo platónico Menón, Sócrates demuestra su Teoría
de Reminiscencia con el siguiente argumento:
``Mi teoría quedaría demostrada si hubiera un individuo con conocimientos innatos. Ahora bien, Menón posee un esclavo con conocimientos de geometrha pues es capaz de construir polhgonos regulares de madera. El esclavo debió adquirir esos conocimientos bien en el transcurso de su vida o bien de manera innata. Pero en el transcurso de su vida no los adquirió pues nunca fué educado. Por tanto, mi teoría es válida''.
Reduzca este argumento al Cálculo de Proposiciones y compruebe en él la validez del razonamiento de Sócrates.
14. Dadas las premisas:
- Si todo primo entre 1 y 101 divide a 101 entonces algún primo menor que 11 divide a 101.
- Hay primos menores que 11 y ninguno de ellos divide a 101.
decida si la siguiente proposición es una consecuencia de ellas
- Algún primo entre 1 y 101 divide a 101.
15. Escriba en el Cálculo de Proposiciones una proposición
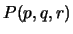 , en términos de las tres básicas
, en términos de las tres básicas 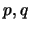 y
y 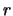 , que sea equivalente a aseverar que dos de ellas son verdaderas y la tercera falsa y además que esté en forma conjuntiva.
, que sea equivalente a aseverar que dos de ellas son verdaderas y la tercera falsa y además que esté en forma conjuntiva.
16. Bruno Torelli, dueño del bar ``La Escondida'', fue muerto a tiros por no pagar puntualmente su cuota de protección. Se detiene a 5 sospechosos, entre los que está el único asesino: Luis, Ramón,
Damián, Sebastián y Tomás. En su comparescencia ante el Juez cada uno hace tres afirmaciones, de las cuales dos son ciertas y una es falsa:
¿Quién fué el culpable?
Sugerencia: Conjeture quién es el culpable. Después demuéstrelo por refutación. Por supuesto, puede incluir otras suposiciones razonables.
17. Falacia ``Afirmación del consecuente''. Una falacia es un esquema de inferencia que parece válido pero no lo es. La seudoregla afirmación del consecuente es la siguiente:
Una instancia de esta seudoregla es, por ejemplo, si le gusto, me mirará; me miró; entonces ¡me ama!.
Vea que esta regla es una falacia encontrando una asignación que haga falsa a la proposicición
Ilustre con un ejemplo en lenguaje natural que puede haber discursos irrebatiblemente válidos que se adecúen a esta seudoregla.
18. Falacia ``Negación del antecedente''. La seudoregla negación del antecedente es la siguiente:
Una instancia de esta seudoregla es, por ejemplo, si la mañana está radiante, ella está contenta; la mañana está nublada; por eso está enojada.
Vea que esta regla es una falacia encontrando una asignación que haga falsa a la proposicición
Ilustre con un ejemplo en lenguaje natural que puede haber discursos irrebatiblemente válidos que se adecúen a esta seudoregla.
19. Falacia del ``Medio No-Distribuído''. La seudoregla del medio no-distribuído es la siguiente:
Una instancia de esta seudoregla es, por ejemplo, si Hugo Sánchez dirige a la Selección, México ganará el Mundial; si Ronaldo se hace mexicano, México ganará el Mundial; así que si Hugo Sánchez dirige a la Selección, Ronaldo se hace mexicano.
Vea que esta regla es una falacia encontrando una asignación que haga falsa a la proposicición
Ilustre con un ejemplo en lenguaje natural que puede haber discursos irrebatiblemente válidos que se adecúen a esta seudoregla.
20. Sea 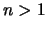 un entero y sea
un entero y sea
![$k\in[\![0,n]\!]$](img951.png) . Para cada punto
. Para cada punto
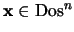 cuente cuántos cubos de dimensión
cuente cuántos cubos de dimensión 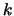 contienen al punto
contienen al punto 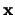 .
.



Posterior: Sintaxis
Arriba: Cálculo proposicional
Anterior: Algoritmo de Quine-McCluskey
Guillermo Morales-Luna
2004-07-27