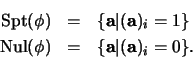Entrada:
Salida:
Algoritmo: Dada una proposición
- Si es ``
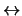 '' o ``
'' o ``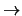 '' transforme
'' transforme  a
una proposición equivalente
a
una proposición equivalente 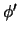 en términos de
en términos de
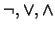 , según las fórmulas
, según las fórmulas
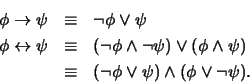
Tendremos
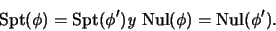
- Si es ``
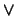 '' entonces
'' entonces  es de la forma
es de la forma
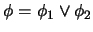 .
En este caso,
.
En este caso,
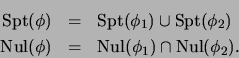
- Si es ``
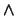 '' entonces
'' entonces  es de la forma
es de la forma
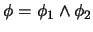 .
En este caso,
.
En este caso,
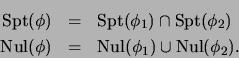
- Si es ``
 '', entonces
'', entonces  es de la forma
es de la forma
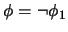 .
En este caso,
.
En este caso,
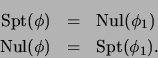
- Si no hubiera conectivos, entonces
 ha de ser una variable
proposicional
ha de ser una variable
proposicional 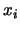 .
En este caso,
.
En este caso,