Posterior: Incompletitud Arriba: Irresolubilidad en la Aritmética Anterior: Irresolubilidad en la Aritmética

Aritmética de Peano

En las tablas 3.6 y 3.7 presentamos dos signaturas para la ARITMÉTICA DE PEANO, sin embargo, en la presentación ulterior de la aritmética de Peano supondremos la signatura de la tabla 3.6.

Table: Signatura $\mbox{\it AP}$ de la Aritmética de Peano.

Table: Signatura $\mbox{\it AP}_1$ de la Aritmética de Peano.

En la aritmética de Peano, se introduce la relación de desigualdad como una fórmula:

$$(x\leq y)\equiv \exists z(x+z=y).$$

Con esto, sea $P^-$ el conjunto de los siguientes axiomas propios:

$$\begin{array}{l\vert l} \begin{array}[t]{c} s(x)\not= 0 \\ ... ...x\cdot z \\ x+y=x+z \rightarrow y=z \end{array} \end{array}$$

Sea $\mbox{\it AP}=P^-\cup \mbox{\it EI}$, donde EI es el ESQUEMA DE INDUCCIÓN: Para cualquier fórmula $\phi$,

$$\phi(0,\mbox{\bf x})\land\forall x(\phi(x,\mbox{\bf x})\right... ...),\mbox{\bf x})) \rightarrow \forall x(\phi(x,\mbox{\bf x})).$$

Ejemplo 5.1   $({\mathbb{N}},\mbox{\it id})$ es una estructura-AP, donde ${\mathbb{N}}$ es el conjunto de números naturales e id es la interpretación usual de los símbolos aritméticos.

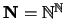
Ejemplo 5.2   El conjunto de funciones de los naturales en los naturales $\mbox{\bf N}={\mathbb{N}}^{{\mathbb{N}}}$ es una estructura-AP con la interpretación de los símbolos ``punto-a-punto'':

Cero $0$	:	$\Phi(0)=\mbox{\bf0}$, donde $\mbox{\bf0}:n\mapsto 0$ es la función cero,
Sucesor $s$	:	$\Phi(s):f\mapsto f'$, donde $f':n\mapsto s(f(n))$ es la función $f+1$,
Suma $+$	:	$\Phi(+):(f,g)\mapsto f+g$, donde $f+g:n\mapsto f(n)+g(n)$ es la función suma punto-a-punto,
Igualdad $=$	:	$\Phi(=)=\{(f,g)\vert\forall n:f(n)=g(n)\}$, es decir, dos funciones son iguales si lo son sus correspondientes valores en cada punto.

Presentaremos una tercer estructura de AP. El FILTRO DE FRÈCHET ${\cal F}=\left\{\left\{m\in{\mathbb{N}}\vert m\geq n\right\}\right\}_{n\in{\mathbb{N}}}$ es, en efecto, un filtro.

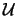
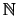
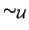
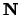
Ejemplo 5.3   Sea ${\cal U}$ un ultrafiltro en ${\mathbb{N}}$ que extienda al filtro de Frèchet y sea $\sim_{{\cal U}}$ la relación en $\mbox{\bf N}$ definida como

$$f\sim_{{\cal U}} g\ \Leftrightarrow\ \{n\in{\mathbb{N}}\vert f(n)=g(n)\}\in U.$$

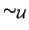
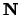
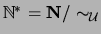
$\sim_{{\cal U}}$ es una relación de equivalencia congruente con las operaciones de $\mbox{\bf N}$ y por tanto ${\mathbb{N}}^*=\mbox{\bf N}/\sim_{{\cal U}}$ es una estructura-AP.

Por ejemplo, la fórmula de la aritmética de Peano

$$\phi_0 \equiv \forall x(x\not=0\rightarrow\exists y(s(y)=x)$$

que asevera que todo elemento no nulo posee un antecesor es válida en ${\mathbb{N}}$, no lo es en $\mbox{\bf N}$ pues la función $x\mapsto(x\mbox{\rm mod }2)$ es no-nula mas no posee antecesor alguno. Sin embargo, $\phi_0$ sí es verdadera en ${\mathbb{N}}^*$.
Posterior: Incompletitud Arriba: Irresolubilidad en la Aritmética Anterior: Irresolubilidad en la Aritmética