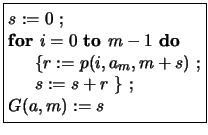next up previous
Posterior: La conjetura de Catalan Arriba: El teorema de Goodstein Anterior: Resolución del sistema de

$G(a,m)$ con $a<m^m$

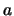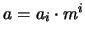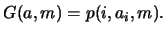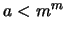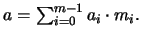Hemos visto que si $a$ es de la forma $a=a_i\cdot m^i$ entonces $G(a,m)=p(i,a_i,m).$ Ahora, si $a<m^m$ tenemos que $\exists a_0,\ldots,a_{m-1}\in[0,m-1]$ tales que $a=\sum_{i=0}^{m-1} a_i\cdot m_i.$ En este caso, 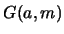$G(a,m)$ es el número de veces que hay que aplicar la construcción de Goodstein para anular a todos los dígitos 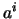$a^i$. Teniendo en cuenta que en cada iteración se incrementa la base, vemos que 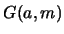$G(a,m)$ se calcula mediante el algoritmo siguiente:
\fbox{\begin{minipage}{20em} \begin{tabbing}123\=456\=789\=012\=345\=678\=901\=... ...,m+s)$\ ; \\ \>$s:=s+r$\ \} ; \\ $G(a,m):= s$ \end{tabbing} \end{minipage}}

Guillermo Morales-Luna
2004-07-27