

Next:ImplementaciónUp:Computational
experiments on thePrevious:Basic
definitions
Main facts
Proposition 3.1 (Necessity [3])
If an AS 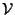 is m-ideal for some m, then there is connected matroid
is m-ideal for some m, then there is connected matroid  appropriate for
appropriate for 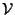 .
.
The reciprocal requires an extra assumption:
Proposition 3.2 (Sufficiency [3])
Let q=pm be a prime power and let 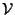 be an AS. Suppose there is connected matroid
be an AS. Suppose there is connected matroid  appropriate for
appropriate for 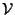 .
.
If  is representable, then
is representable, then 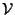 is q-ideal.
is q-ideal.
Indeed, there is a beautiful characterization of universal-ideality:
Proposition 3.3 ([1])
An AS 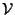 is universally-ideal if and only if
is universally-ideal if and only if 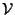 is 2-ideal and 3-ideal.
is 2-ideal and 3-ideal.
Open problem
If there is a connected matroid  appropriate for an AS which is not representable over the field
appropriate for an AS which is not representable over the field 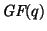 ,
decide whether the AS is q-ideal.
,
decide whether the AS is q-ideal.
Regarding graphs, G=(V,E) let 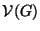 be the collection of sets that include at least one edge:
be the collection of sets that include at least one edge:

Then the following conditions are pairwise equivalent:
-
1.
-
G=(V,E) is a multipartite graph, i.e. there is a partition
![$\left[V_k\right]_k$](img65.gif) of V such that
of V such that
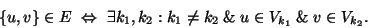
-
2.
-
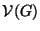 is I-ideal.
is I-ideal.
-
3.
-
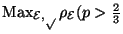 .
.
-
4.
-
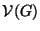 has an appropriate representable matroid.
has an appropriate representable matroid.
Inmediately a procedure to build a SSS follows:
-
1.
-
Given a set of participants V and a collection
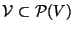 ,
,
-
2.
-
decide whether
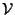 has an appropriate matroid
has an appropriate matroid  ,
,
-
3.
-
if
 is representable, then construct the corresponding SSS according to Shamir's
procedure.
is representable, then construct the corresponding SSS according to Shamir's
procedure.
We are building an experimentation computational system to deal with
the following problems:
-
1.
-
Representation of matroids.
-
2.
-
Random selection of a matroid over the whole possibilities to pick a matroid
over a ground set of n participants.
-
3.
-
Given a collection
![${\cal V}\in {\cal P}({\cal P}([\![1,n]\!]))$](img68.gif) whose elements are of the same cardinality, say k, decide whether
there is a matroid of rank k whose bases are the elements in
whose elements are of the same cardinality, say k, decide whether
there is a matroid of rank k whose bases are the elements in 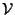 .
.
-
4.
-
Decide whether a matroid is representable over a finite field.
-
5.
-
Specify a general procedure to build an ideal SSS provided a representable
matroid.


Next:ImplementaciónUp:Computational
experiments on thePrevious:Basic
definitions
Guillermo Morales-Luna
2000-11-28
![]() be an AS. Suppose there is connected matroid
be an AS. Suppose there is connected matroid ![]() appropriate for
appropriate for ![]() .
.
![]() is representable, then
is representable, then ![]() is q-ideal.
is q-ideal.
![]() is universally-ideal if and only if
is universally-ideal if and only if ![]() is 2-ideal and 3-ideal.
is 2-ideal and 3-ideal.
![]() appropriate for an AS which is not representable over the field
appropriate for an AS which is not representable over the field ![]() ,
decide whether the AS is q-ideal.
,
decide whether the AS is q-ideal.
![]() be the collection of sets that include at least one edge:
be the collection of sets that include at least one edge: