Siguiente: Primeras listas
Arriba: Códigos de Huffman
Anterior: Códigos de Huffman terciarios,
Dada una palabra 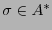 , la frecuencia
, la frecuencia
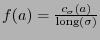 de un símbolo
de un símbolo 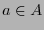 puede identificarse como la probabilidad de que ocurra
puede identificarse como la probabilidad de que ocurra 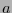 . Si
. Si
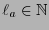 es la longitud del código de
es la longitud del código de 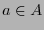 entonces la longitud esperada del código de Huffman es
entonces la longitud esperada del código de Huffman es
Escribamos 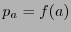 .
.
La función de entropía
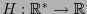 se define de manera que cumpla con las propiedades siguientes:
se define de manera que cumpla con las propiedades siguientes:
- Positiva.
-
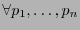 :
:
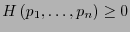 .
.
- Contínua.
-
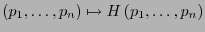 es contínua.
es contínua.
- Simétrica.
-
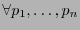 ,
,
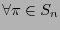 :
:
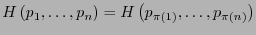 .
.
- Coherente.
-
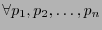 :
:
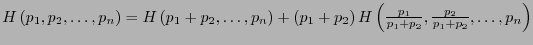 .
.
Para esto se debe tener que existe 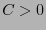 tal que
tal que
donde se ha de entender:
![$\left[p=0\ \Rightarrow\ p \log \frac{1}{p}=0.\right]$](img171.png) . Al expresar
. Al expresar
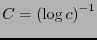 , se ha de tener
, se ha de tener
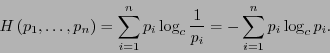 |
(6) |
Esta última expresión define la llamada entropía de Shannon, considerando 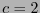 .
Para el caso
.
Para el caso 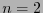 , la relación (6) queda
, la relación (6) queda
Esta función es tal que
![$H([0,1]) = [0,1]$](img177.png) , posee sus valores mínimos en
, posee sus valores mínimos en 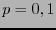 (que una frecuencia sea 1 significa que en la cadena original sólo ha de aparecer un símbolo) y su valor máximo en
(que una frecuencia sea 1 significa que en la cadena original sólo ha de aparecer un símbolo) y su valor máximo en 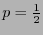 (los símbolos que aparecen en la cadena original son equiprobables).
(los símbolos que aparecen en la cadena original son equiprobables).
Sea
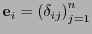 el
el 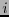 -ésimo vector canónico que tiene el valor 1 en la
-ésimo vector canónico que tiene el valor 1 en la 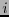 -ésima coordenada y el valor 0 en las otras. Este corresponde a la distribución de probabilidad en la que sólo aparece el
-ésima coordenada y el valor 0 en las otras. Este corresponde a la distribución de probabilidad en la que sólo aparece el 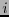 -ésimo símbolo y ninguno otro. Pues bien, de la relación (6) se ve que
-ésimo símbolo y ninguno otro. Pues bien, de la relación (6) se ve que
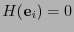 , lo que da una mínima entropía. Si se considera
, lo que da una mínima entropía. Si se considera
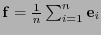 , que corresponde a la distribución uniforme de probabilidad, se tiene
, que corresponde a la distribución uniforme de probabilidad, se tiene
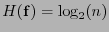 , lo que da una máxima entropía.
, lo que da una máxima entropía.
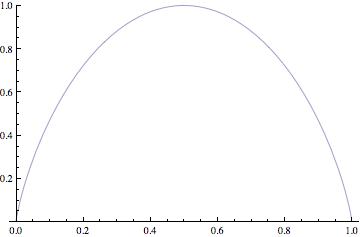
En la figura 1 presentamos las gráficas de 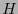 para alfabetos de dos y de tres símbolos respectivamente.
para alfabetos de dos y de tres símbolos respectivamente.
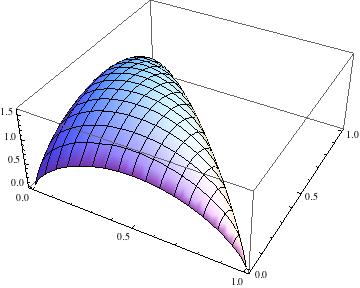
Figura 1:
Gráfica de la función de entropía de Shannon.
| Dos símbolos |
 |
| Tres símbolos |
 |
|
Supongamos que
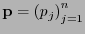 es la distribución de probabilidad de un alfabeto
es la distribución de probabilidad de un alfabeto 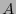 de
de  símbolos, y que
símbolos, y que
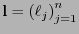 es la lista de longitudes de un código instantáneo de
es la lista de longitudes de un código instantáneo de 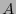 . Entonces la longitud esperada ha de ser
. Entonces la longitud esperada ha de ser
![$E({\bf l}) = \sum_{j=1}^n \ell_jp_j = \sum_{j=1}^n p_j\log_2\left[2^{\ell_j}\right]$](img187.png) y, en consecuencia
y, en consecuencia
de donde
(donde la última es precisamente la desigualdad de Kraft). Así pues,
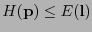 , es decir la longitud esperada de cualquier código instantáneo es mayor o igual que la entropía de la distribución de probabilidad de los símbolos.
, es decir la longitud esperada de cualquier código instantáneo es mayor o igual que la entropía de la distribución de probabilidad de los símbolos.
Para una distribución
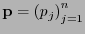 de un alfabeto
de un alfabeto 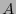 de
de  símbolos y un entero positivo
símbolos y un entero positivo 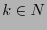 , se define la distribución
, se define la distribución 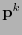 sobre el alfabeto
sobre el alfabeto 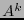 , que consiste de las palabras de longitud
, que consiste de las palabras de longitud 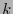 , haciendo
, haciendo
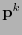 se dice ser la
se dice ser la 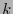 -ésima extensión de
-ésima extensión de 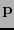 .
.
Se tendrá entonces que vale el
Teorema 3.1 (de Shannon de Códigos sin Ruido)
Para cualquier distribución de probabilidad 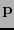 , sea
, sea
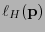 la longitud esperada de una codificación de Huffman. Entonces
Y para extensiones sucesivas,
la longitud esperada de una codificación de Huffman. Entonces
Y para extensiones sucesivas,
Planteemos un caso de estudio que se resolvería de manera directa utilizando el teorema de Shannon 3.1.
Ejemplo 3.2
Supongamos que se quiere transmitir un croquis. Este está conformado prácticamente por unas cuantas líneas sobre fondo blanco. Al digitalizar la imagen, la probabilidad de que aparezca un 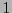 (pixel negro) es a lo sumo
(pixel negro) es a lo sumo 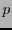 y de que aparezca
y de que aparezca 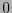 (pixel blanco) es al menos
(pixel blanco) es al menos 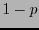 , con
, con 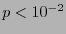 , digamos. El alfabeto original
, digamos. El alfabeto original 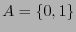 consta de dos símbolos. Para
consta de dos símbolos. Para 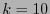 , se divide la imagen en bloques de
, se divide la imagen en bloques de 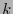 pixeles consecutivos. El alfabeto actual es entonces
pixeles consecutivos. El alfabeto actual es entonces 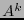 . A toda cadena de ceros,
. A toda cadena de ceros, 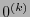 , se la codifica con un solo
, se la codifica con un solo 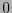 , y a cualquier otra cadena
, y a cualquier otra cadena 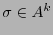 con la cadena
con la cadena
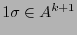 . ¿Cuál es la esperanza de la longitud del código?
. ¿Cuál es la esperanza de la longitud del código?
La longitud esperada del código de una cadena 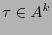 es
es
así esta longitud será más cercana a 1 conforme 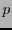 sea más pequeño, o sea la compresión será mayor (de
sea más pequeño, o sea la compresión será mayor (de 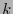 a 1). El teorema de Shannon 3.1 da la misma estimación de manera más directa y general.
a 1). El teorema de Shannon 3.1 da la misma estimación de manera más directa y general.




Siguiente: Primeras listas
Arriba: Códigos de Huffman
Anterior: Códigos de Huffman terciarios,
Guillermo M. Luna
2010-05-09
![]() , la frecuencia
, la frecuencia
![]() de un símbolo
de un símbolo ![]() puede identificarse como la probabilidad de que ocurra
puede identificarse como la probabilidad de que ocurra ![]() . Si
. Si
![]() es la longitud del código de
es la longitud del código de ![]() entonces la longitud esperada del código de Huffman es
entonces la longitud esperada del código de Huffman es
![]() se define de manera que cumpla con las propiedades siguientes:
se define de manera que cumpla con las propiedades siguientes:
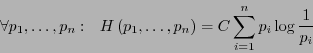
![]() el
el ![]() -ésimo vector canónico que tiene el valor 1 en la
-ésimo vector canónico que tiene el valor 1 en la ![]() -ésima coordenada y el valor 0 en las otras. Este corresponde a la distribución de probabilidad en la que sólo aparece el
-ésima coordenada y el valor 0 en las otras. Este corresponde a la distribución de probabilidad en la que sólo aparece el ![]() -ésimo símbolo y ninguno otro. Pues bien, de la relación (6) se ve que
-ésimo símbolo y ninguno otro. Pues bien, de la relación (6) se ve que
![]() , lo que da una mínima entropía. Si se considera
, lo que da una mínima entropía. Si se considera
![]() , que corresponde a la distribución uniforme de probabilidad, se tiene
, que corresponde a la distribución uniforme de probabilidad, se tiene
![]() , lo que da una máxima entropía.
, lo que da una máxima entropía.
![]() para alfabetos de dos y de tres símbolos respectivamente.
para alfabetos de dos y de tres símbolos respectivamente.
![]() es la distribución de probabilidad de un alfabeto
es la distribución de probabilidad de un alfabeto ![]() de
de ![]() símbolos, y que
símbolos, y que
![]() es la lista de longitudes de un código instantáneo de
es la lista de longitudes de un código instantáneo de ![]() . Entonces la longitud esperada ha de ser
. Entonces la longitud esperada ha de ser
![]() y, en consecuencia
y, en consecuencia
![\begin{displaymath}H({\bf p}) - E({\bf l}) = \sum_{j=1}^n p_j\log_2\left[\frac{1...
...\log 2}\sum_{j=1}^n p_j\log\left[\frac{1}{2^{\ell_j}p_j}\right]\end{displaymath}](img188.png)
![\begin{displaymath}H({\bf p}) - E({\bf l}) \leq \frac{1}{\log 2}\sum_{j=1}^n p_j...
...\frac{1}{\log 2}\left[\sum_{j=1}^n 2^{-\ell_j} -1\right] \leq 0\end{displaymath}](img189.png)
![]() de un alfabeto
de un alfabeto ![]() de
de ![]() símbolos y un entero positivo
símbolos y un entero positivo ![]() , se define la distribución
, se define la distribución ![]() sobre el alfabeto
sobre el alfabeto ![]() , que consiste de las palabras de longitud
, que consiste de las palabras de longitud ![]() , haciendo
, haciendo
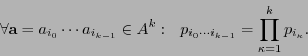
![]() es
es