



Siguiente: Pesos mínimos
Arriba: Códigos lineales
Anterior: Códigos lineales
Sea 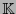 un campo cualquiera finito, de cardinalidad, digamos,
un campo cualquiera finito, de cardinalidad, digamos, 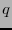 , el cual es, por consiguiente, una potencia de la característica de
, el cual es, por consiguiente, una potencia de la característica de 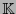 . Para cada
. Para cada 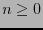 denotemos por
denotemos por 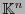 a su
a su  -ésima potencia cartesiana dotada de su estructura usual de espacio vectorial sobre el campo
-ésima potencia cartesiana dotada de su estructura usual de espacio vectorial sobre el campo 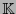 .
.
Definición 5.1
Todo subespacio
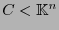 de dimensión
de dimensión 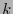 es un código lineal-
es un código lineal-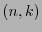 sobre el alfabeto
sobre el alfabeto 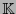 .
.
Todo código lineal-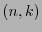 tiene
tiene 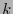 símbolos de información y
símbolos de información y 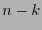 símbolos de revisión. Está conformado por
símbolos de revisión. Está conformado por 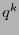 palabras de código.
palabras de código.
Si
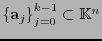 es una base de
es una base de  , la matriz
, la matriz
![$A=\left[{\bf a}_j\right]_{j=0}^{k-1}\in\mathbb{K}^{n\times k}$](img471.png) , cuyas columnas son los vectores en la base, se dice ser generatriz del código
, cuyas columnas son los vectores en la base, se dice ser generatriz del código  . En tal caso, la transformación
. En tal caso, la transformación
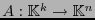 ,
,
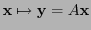 , tiene como imagen a
, tiene como imagen a  precisamente. Mediante la aplicación de una transformación lineal de permutación
precisamente. Mediante la aplicación de una transformación lineal de permutación 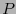 en el espacio
en el espacio 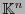 , se tiene
, se tiene 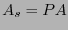 donde
donde 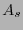 es una matriz generatriz de la forma
es una matriz generatriz de la forma
![$A_s=\left[\begin{array}{c} I_{k} \\ A_r\end{array}\right]$](img477.png) , con
, con
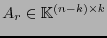 , llamada sistemática.
, llamada sistemática.
Definición 5.2
Dos códigos  y
y 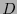 se dicen equivalentes si una generatriz de uno se obtiene mediante la aplicación de una matriz de permutación a la generatriz del otro.
se dicen equivalentes si una generatriz de uno se obtiene mediante la aplicación de una matriz de permutación a la generatriz del otro.
Así todo código lineal es equivalente a otro con una generatriz sistemática.
Definición 5.3
Una matriz
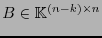 es revisora de paridad para un código lineal-
es revisora de paridad para un código lineal-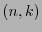
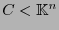 si se cumple:
si se cumple:
Se tiene, de manera natural:
Por tanto se tiene que toda matriz revisora de paridad posee rango 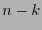 .
.
Definición 5.4
Dado un código lineal-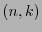
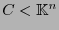 , su código dual es
, su código dual es
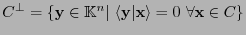 .
.
Naturalmente, la matriz revisora de paridad de un código es la generatriz del dual y, viceversa, la generatriz es la revisora de paridad del dual.
Definición 5.5
Si
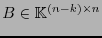 es la matriz revisora de paridad de un código lineal-
es la matriz revisora de paridad de un código lineal-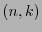
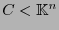 entonces la transformación lineal
entonces la transformación lineal
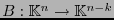 ,
,
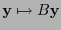 , se dice ser de síndrome.
El valor
, se dice ser de síndrome.
El valor 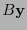 es el síndrome de la palabra
es el síndrome de la palabra 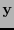 .
.
Así tenemos que las palabras en el código son exactamente aquellas con síndrome nulo. En otras palabras, el núcleo de la transformación de síndrome es el código mismo.




Siguiente: Pesos mínimos
Arriba: Códigos lineales
Anterior: Códigos lineales
Guillermo M. Luna
2010-05-09
![]() un campo cualquiera finito, de cardinalidad, digamos,
un campo cualquiera finito, de cardinalidad, digamos, ![]() , el cual es, por consiguiente, una potencia de la característica de
, el cual es, por consiguiente, una potencia de la característica de ![]() . Para cada
. Para cada ![]() denotemos por
denotemos por ![]() a su
a su ![]() -ésima potencia cartesiana dotada de su estructura usual de espacio vectorial sobre el campo
-ésima potencia cartesiana dotada de su estructura usual de espacio vectorial sobre el campo ![]() .
.
![]() es una base de
es una base de ![]() , la matriz
, la matriz
![]() , cuyas columnas son los vectores en la base, se dice ser generatriz del código
, cuyas columnas son los vectores en la base, se dice ser generatriz del código ![]() . En tal caso, la transformación
. En tal caso, la transformación
![]() ,
,
![]() , tiene como imagen a
, tiene como imagen a ![]() precisamente. Mediante la aplicación de una transformación lineal de permutación
precisamente. Mediante la aplicación de una transformación lineal de permutación ![]() en el espacio
en el espacio ![]() , se tiene
, se tiene ![]() donde
donde ![]() es una matriz generatriz de la forma
es una matriz generatriz de la forma
![$A_s=\left[\begin{array}{c} I_{k} \\ A_r\end{array}\right]$](img477.png) , con
, con
![]() , llamada sistemática.
, llamada sistemática.